题目内容
12．设函数$f（x）=\left\{{\begin{array}{l}{\sqrt{x-1}}&{x≥1}\\ 1&{x＜1}\end{array}}\right.$，则$f（{f（{f（{\frac{π}{2}}）}）}）$的值为（ ）| A． | 0 | B． | 1 | C． | $\sqrt{\frac{π}{2}-1}$ | D． | $\sqrt{\sqrt{\frac{π}{2}-1}-1}$ |
分析 直接利用导函数由里及外逐步求解即可．
解答 解：函数$f（x）=\left\{{\begin{array}{l}{\sqrt{x-1}}&{x≥1}\\ 1&{x＜1}\end{array}}\right.$，
则$f（{f（{f（{\frac{π}{2}}）}）}）$=f（f（$\sqrt{\frac{π}{2}-1}$））=f（1）=$\sqrt{1-1}$=0．
故选：A．
点评 本题考查分段函数的应用，函数值的求法，考查计算能力．
练习册系列答案
相关题目
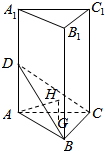如图所示，三棱柱ABC-A1B1C1的底面是正三角形，侧棱AA1⊥底面ABC，AB=1，AA1=2，点D在侧棱AA1上，点G，H分别是△ABC，△BCD的重心．
2．下列积分均存在，则下列结论错误的是（ ）
| A． | d（∫f（x）dx）=f（x）dx | B． | ∫f（x）dx=∫f（u）du | ||
| C． | ${∫}_{a}^{b}$f（x）dx=${∫}_{a}^{b}$f（u）du | D． | ${∫}_{a}^{b}$f（x）dx+${∫}_{b}^{a}$f（x）dx=0． |