题目内容
在△ABC中,a2tanB=b2tanA,则△ABC是__________( )
| A、等腰或直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
考点:三角形的形状判断
专题:解三角形
分析:利用正弦定理化简,可得sin2A=sin2B,从而可得2A=2B或2A+2B=π,即可得出结论.
解答:
解:∵a2tanB=b2tanA,
∴sin2AtanB=sin2BtanA,
∴sinAcosA=sinBcosB,
∴sin2A=sin2B,
∴2A=2B或2A+2B=π,
∴A=B或A+B=
,
∴△ABC是等腰或直角三角形.
故选A.
∴sin2AtanB=sin2BtanA,
∴sinAcosA=sinBcosB,
∴sin2A=sin2B,
∴2A=2B或2A+2B=π,
∴A=B或A+B=
| π |
| 2 |
∴△ABC是等腰或直角三角形.
故选A.
点评:本题考查正弦定理的运用,考查三角形形状的判断,正确运用正弦定理是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式的值大于
的是( )
| 3 |
| 2 |
A、cos
| ||||||
| B、sin810°+tan765°-cos360° | ||||||
| C、sin(-1740°)cos1470°+cos(-660°)sin750°+tan405° | ||||||
D、sin 2
|
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| 4×6 |
| 1 |
| n(n+2) |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
定义在(1,+∞)上的函数f(x)满足两个条件:(1)对任意的x∈(1,+∞)恒有f(2x)=2f(x)成立;(2)当x∈(1,2)时,f(x)=2-x;记函数g(x)=f(x)-k(x-1),若函数g(x)恰有两个零点,则实数k的取值范围是( )
| A、(1,2) | ||
B、(1,
| ||
C、(
| ||
D、(
|
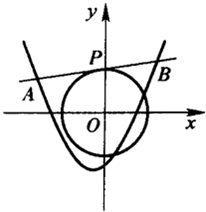 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;