题目内容
已知向量
，
满足：|
|=2，|
|=1，且
•
=2，则|
+
|为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | B、4 | C、9 | D、8 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积的性质即可得出．
解答：
解：∵|
|=2，|
|=1，且
•
=2，
∴|
+
|=
=
=3．
故选：A．
| a |
| b |
| a |
| b |
∴|
| a |
| b |
|
| 22+12+2×2 |
故选：A．
点评：本题考查了数量积的性质，属于基础题．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
已知a，b为正实数且ab=1，若不等式（x+y）（
+
）＞M对任意正实数x，y恒成立，则实数M的取值范围是（ ）
| a |
| x |
| b |
| y |
| A、[4，+∞） |
| B、（-∞，1] |
| C、（-∞，4] |
| D、（-∞，4） |
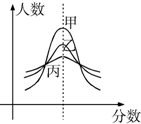某市期末教学质量检测，甲、乙、丙三科考试成绩近似服从正态分布，则由如图曲线可得下列说法中正确的是（ ）| A、甲学科总体的方差最小 |
| B、丙学科总体的均值最小 |
| C、乙学科总体的方差及均值都居中 |
| D、甲、乙、丙的总体的均值不相同 |
在等差数列{an}中，a2=2，a6=8，则a10的值为（ ）
| A、10 | B、12 | C、14 | D、16 |
已知a=cos234°-sin234°，b=2sin78°cos78°，c=
，则有（ ）
| 2tan12° |
| 1-tan212° |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、c＞b＞a |
用二分法求方程f（x）=0在（1，2）内近似解的过程中得f（1）＜0，f（1.5）＞0，f（1.25）＜0，则方程的根在区间（ ）
| A、（1.25，1.5） |
| B、（1，1.25） |
| C、（1.5，2） |
| D、不能确定 |
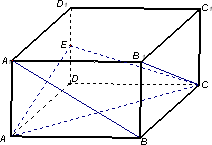在长方体ABCD-A1B1C1D1中，已知DA=DC=4，DD1=3，E是DD1的中点