题目内容
如图,在三棱柱ABC-A1B1C1中,A1A⊥ 平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
(1)当F为A1A的中点,求直线BC与平面BFC1所成角的正弦值;
(2)当
的值为多少时,二面角B-FC1-C的大小是45°.
 平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.(1)当F为A1A的中点,求直线BC与平面BFC1所成角的正弦值;
(2)当
| AF |
| FA1 |
考点:与二面角有关的立体几何综合题,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)以点A为原点建立空间直角坐标系,利用向量法能求出直线BC与平面BFC1所成角的正弦值.
(2)求出平面BFC1的一个法向量,利用向量法能求出当
=
时,二面角B-FC1-C的大小是45°.
(2)求出平面BFC1的一个法向量,利用向量法能求出当
| AF |
| FA1 |
| 5 |
| 3 |
解答:
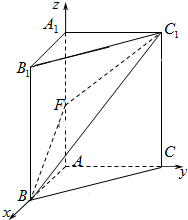 解:(1)如图,以点A为原点建立空间直角坐标系,
解:(1)如图,以点A为原点建立空间直角坐标系,
依题意得A(0,0,0),B(2,0,0),C(0,2,0),
A1(0,0,4),C1(0,2,4),∵F为AA1r 中点,
∴F(0,0,2),
=(-2,0,2),
=(-2,2,4),
=(-2,2,0),
设
=(x,y,z)是平面BFC1的一个法向量,
则
,得x=-y=z
取x=1,得
=(1,-1,1),
设直线BC与平面BFC1的法向量
=(1,-1,1)的夹角为θ,
则cosθ=
=
=-
,
∴直线BC与平面BFC1所成角的正弦值为
.
(2)设F(0,0,t)(0≤t≤4),
=(-2,0,t),
=(-2,2,4),
设
=(x,y,z)是平面BFC1的一个法向量,
则
,
取z=2,得
=(t,t-4,2)
=(2,0,0)是平面FC1C的一个法向量,cos<
,
>=
=
=
,
得t=
,即AF=
,FA1=
,
∴当
=
时,二面角B-FC1-C的大小是45°.
 解:(1)如图,以点A为原点建立空间直角坐标系,
解:(1)如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),B(2,0,0),C(0,2,0),
A1(0,0,4),C1(0,2,4),∵F为AA1r 中点,
∴F(0,0,2),
| BF |
| BC1 |
| BC |
设
| n |
则
|
取x=1,得
| n |
设直线BC与平面BFC1的法向量
| n |
则cosθ=
| ||||
|
|
| -4 | ||||
2
|
| ||
| 3 |
∴直线BC与平面BFC1所成角的正弦值为
| ||
| 3 |
(2)设F(0,0,t)(0≤t≤4),
| BF |
| BC1 |
设
| n |
则
|
取z=2,得
| n |
| AB |
| n |
| AB |
| ||||
|
|
| 2t | ||
2
|
| ||
| 2 |
得t=
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
∴当
| AF |
| FA1 |
| 5 |
| 3 |
点评:本题考查直线与平面所成角的正弦值的求法,考查二面角为45°时点的位置的确定,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
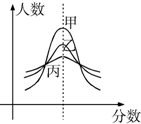 某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中正确的是( )
某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中正确的是( )| A、甲学科总体的方差最小 |
| B、丙学科总体的均值最小 |
| C、乙学科总体的方差及均值都居中 |
| D、甲、乙、丙的总体的均值不相同 |
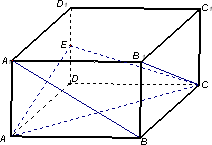 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,E是DD1的中点
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,E是DD1的中点