题目内容
设函数g（x）=3x，h（x）=9x．
（1）解方程：x+log3（2g（x）-8）=log3（h（x）+9）；
（2）令p（x）=
，q（x）=
，求证：p（
）+p（
）+…+p（
）+p（
）=q（
）+q（
）+…+q（
）+q（
）
（3）若f（x）=
是实数集R上的奇函数，且f（h（x）-1）+f（2-k•g（x））＞0对任意实数x恒成立，求实数k的取值范围．
（1）解方程：x+log3（2g（x）-8）=log3（h（x）+9）；
（2）令p（x）=
| g(x) | ||
g(x)+
|
| 3 |
| h(x)+3 |
| 1 |
| 2014 |
| 2 |
| 2014 |
| 2012 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
| 2 |
| 2014 |
| 2012 |
| 2014 |
| 2013 |
| 2014 |
（3）若f（x）=
| g(x+1)+a |
| g(x)+b |
考点：对数函数图象与性质的综合应用
专题：函数的性质及应用
分析：（1）通过观察方程式，很自然的把方程左边变成log33x(2g(x)-8)，这时候就可以把方程中的对数符号去掉了，下面的求解就比较简单了．
（2）通过观察要证的等式，发现等式一边首尾的两个自变量值和为1，比如
+
=1，这时候思考，对应函数值的和是否能于1呢，带入函数式证明是可以的，所以就能够分别求出等式左右的和了，和一样即可．
（3）根据函数是奇函数，便能求出a，b．通过观察不等式f（h（x）-1）+f（2-k•g（x））＞0便容易想到，看能不能用上函数f（x）的单调性，并能说明该函数是单调递增的，不等式f（h（x）-1）+f（2-k•g（x））＞0可以变成，f（h（x）-1）＞-f（2-k•g（x）），再根据奇偶性，变成f（h（x）-1）＞f（k•g（x）-2），这时候就可以用上函数f（x）的单调性，下面对a的范围的求解就比较简单了．
（2）通过观察要证的等式，发现等式一边首尾的两个自变量值和为1，比如
| 1 |
| 2014 |
| 2013 |
| 2014 |
（3）根据函数是奇函数，便能求出a，b．通过观察不等式f（h（x）-1）+f（2-k•g（x））＞0便容易想到，看能不能用上函数f（x）的单调性，并能说明该函数是单调递增的，不等式f（h（x）-1）+f（2-k•g（x））＞0可以变成，f（h（x）-1）＞-f（2-k•g（x）），再根据奇偶性，变成f（h（x）-1）＞f（k•g（x）-2），这时候就可以用上函数f（x）的单调性，下面对a的范围的求解就比较简单了．
解答：
解：（1）将g（x），h（x）带入方程得：
x+log3(2•3x-8)=log3(9x+9)，∵x=log33x；
∴log33x(2•3x-8)=log3(9x+9)；
∴3x（2•3x-8）=（3x）2+9，化简得：（3x+1）（3x-9）=0；
∴x=2．
（2）p(x)=
，q(x)=
；
∴p(
)=p(
)=
=
，q(
)=q(
)=
=
；
∵p（x）+p（1-x）=
+
=
+
=1；
q(x)+q(1-x)=
+
=
+
=1；
∴p(
)+p(
)+…+p(
)+p(
)=1006+
；
q(
)+q(
)+…+q(
)+q(
)=1006+
．
∴原等式成立．
（3）因为f（x）是实数集上的奇函数，所以a=-3，b=1．
∴f(x)=
=3-
，f（x）在实数集上单调递增．
由f（h（x）-1）+f（2-k•g（x））＞0得f（h（x）-1）＞-f（2-k•g（x）），又因为f（x）是实数集上的奇函数，所以，f（h（x）-1）＞f（k•g（x）-2），
又因为f（x）在实数集上单调递增，所以h（x）-1＞k•g（x）-2
即32x-1＞k•3x-2对任意的x∈R都成立，
即k＜
=3x+
对任意的x∈R都成立，
∵3x+
≥2，∴k＜2．
x+log3(2•3x-8)=log3(9x+9)，∵x=log33x；
∴log33x(2•3x-8)=log3(9x+9)；
∴3x（2•3x-8）=（3x）2+9，化简得：（3x+1）（3x-9）=0；
∴x=2．
（2）p(x)=
| 3x | ||
3x+
|
| 3 |
| 9x+3 |
∴p(
| 1007 |
| 2014 |
| 1 |
| 2 |
| ||
2
|
| 1 |
| 2 |
| 1007 |
| 2014 |
| 1 |
| 2 |
| 3 |
| 6 |
| 1 |
| 2 |
∵p（x）+p（1-x）=
| 3x | ||
3x+
|
| 31-x | ||
3x+
|
| 3x | ||
3x+
|
| ||
3x+
|
q(x)+q(1-x)=
| 9x |
| 9x+3 |
| 91-x |
| 91-x+3 |
| 9x |
| 9x+3 |
| 3 |
| 9x+3 |
∴p(
| 1 |
| 2014 |
| 2 |
| 2014 |
| 2012 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2 |
q(
| 1 |
| 2014 |
| 2 |
| 2014 |
| 2012 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2 |
∴原等式成立．
（3）因为f（x）是实数集上的奇函数，所以a=-3，b=1．
∴f(x)=
| 3x+1-3 |
| 3x+1 |
| 6 |
| 3x+1 |
由f（h（x）-1）+f（2-k•g（x））＞0得f（h（x）-1）＞-f（2-k•g（x）），又因为f（x）是实数集上的奇函数，所以，f（h（x）-1）＞f（k•g（x）-2），
又因为f（x）在实数集上单调递增，所以h（x）-1＞k•g（x）-2
即32x-1＞k•3x-2对任意的x∈R都成立，
即k＜
| 32x+1 |
| 3x |
| 1 |
| 3x |
∵3x+
| 1 |
| 3x |
点评：方程中含对数符号，应该想到把对数符号去掉．第二问通过观察要证的等式能发现一边的式子中的首尾项的自变量值为1，并猜想对应函数值是否为1，并去求出这两项的和为1．第三问首先能求出a，b，然后能判断函数的单调性，比较关键的是将f（h（x）-1）+f（2-k•g（x））＞0变成f（h（x）-1）＞f（k•g（x）-2）．
练习册系列答案
相关题目
在△ABC中，若
•
=3
•
，cosC=
，则A的大小为（ ）
| AB |
| AC |
| BA |
| BC |
| ||
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
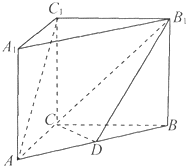如图，在三棱柱ABC-A1B1C1中，C1C⊥底面ABC，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．