题目内容
在锐角△ABC中，内角A，B，C的对边分别为a，b，c．设
=（2a，-b），
=（sinB，
），且
⊥
，则
（1）求角A的大小；
（2）若S△ABC=4
，b+c=8，求边a．
. |
| m |
. |
| n |
| 3 |
. |
| m |
. |
| n |
（1）求角A的大小；
（2）若S△ABC=4
| 3 |
考点：余弦定理,正弦定理
专题：解三角形
分析：（1）根据
⊥
，建立等式求得sinA的值，进而求得A．
（2）先根据三角形面积公式和已知条件求得bc的值，进而利用余弦定理求得a．
. |
| m |
. |
| n |
（2）先根据三角形面积公式和已知条件求得bc的值，进而利用余弦定理求得a．
解答：
解：（1）由已知得到：2sinAsinB=
sinB，且B∈（0，
），
∴sinA=
，
∵A∈（0，
），
∴A=
．
（2）S△ABC=
bcsinA=
bc=4
，
∴bc=16，
∴a=
=
=4
| 3 |
| π |
| 2 |
∴sinA=
| ||
| 2 |
∵A∈（0，
| π |
| 2 |
∴A=
| π |
| 3 |
（2）S△ABC=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
∴bc=16，
∴a=
| b2+c2-2bccosA |
| (b+c)2-3bc |
点评：本题主要考查了余弦定理的应用．考查了学生对三角函数基础知识的灵活运用．
练习册系列答案
口算能手系列答案
相关题目
（文科）sin
π等于（ ）
| 2009 |
| 4 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|
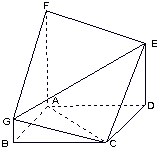如图，多面体ABCDEFG中，FA⊥平面ABCD，FA∥BG∥DE，BG=
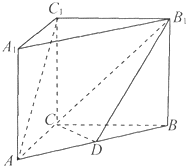如图，在三棱柱ABC-A1B1C1中，C1C⊥底面ABC，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．