题目内容
3.设$a,b,c∈({0,\frac{π}{2}})$,且满足cosa=a,sin(cosb)=b,cos(sinc)=c,则a,b,c的大小关系为b<a<c.分析 先利用导数证明当x∈(0,$\frac{π}{2}$)时,sinx<x,再构造新函数证明f(x)=sin(cosx)-x为(0,$\frac{π}{2}$)上的减函数,g(x)=cos(sinx)-x为(0,$\frac{π}{2}$)上的减函数;最后将x=a分别代入两函数,判断函数值正负,从而利用函数的单调性比较自变量a、b、c的大小
解答 解:先证明当x∈(0,$\frac{π}{2}$)时,sinx<x
设y=sinx-x,则y′=cosx-1<0,∴y=sinx-x为(0,$\frac{π}{2}$)上的减函数,∴y<sino-0=0,即sinx<x
同理可证明f(x)=sin(cosx)-x为(0,$\frac{π}{2}$)上的减函数,g(x)=cos(sinx)-x为(0,$\frac{π}{2}$)上的减函数
∵sina<a
∴cos(sina)-a=cos(sina)-cosa>0,而cos(sinc)-c=0,
∴g(a)>g(c),a、c∈(0,$\frac{π}{2}$),
∴a<c
同理∵x∈(0,$\frac{π}{2}$)时,sinx<x,∴sin(cosa)<cosa
∴sin(cosa)-a=sin(cosa)-cosa<0,而sin(cosb)-b=0
∴f(a)<f(b),a、b∈(0,$\frac{π}{2}$),
∴a>b
综上所述,b<a<c
故答案为b<a<c.
点评 本题考查了利用函数的单调性比较大小的方法,恰当的构造函数,正确的研究其单调性是解决本题的关键.

练习册系列答案
相关题目
13.已知曲线y=$\frac{{x}^{2}}{2}$-3lnx的一条切线的与直线x+2y+10=0垂直,则切点的横坐标为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | 1 | D. | 3 |
11.由1,2,3这三个数字组成的没有重复数字的三位自然数共有( )
| A. | 6个 | B. | 8个 | C. | 12个 | D. | 15个 |
12.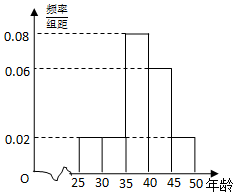 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:
(1)如表是年龄的频数分布表,求a,b的值;
(2)根据频率分布直方图估计志愿者年龄的平均数和中位数;
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的分别抽取多少人?
(4)在(3)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:(1)如表是年龄的频数分布表,求a,b的值;
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的分别抽取多少人?
(4)在(3)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
13.在区间(1,7)上任取一个数,这个数在区间(5,8)上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |