题目内容
12.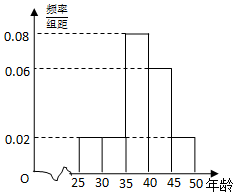 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:(1)如表是年龄的频数分布表,求a,b的值;
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的分别抽取多少人?
(4)在(3)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
分析 (1)根据频率分布直方图求频率,由此能求出a,b的值.
(2)根据频率分布直方图能估计志愿者年龄的平均数和中位数.
(3)利用样本容量比总容量的比例计算.
(4)利用第2问的结论,列出所有可能情况,在其中挑出符合题意的情况,求比值.
解答 解:(1)由频率分布直方图知:
a=0.08×5×500=200,
b=0.02×5×500=50.
(2)由频率分布直方图估计志愿者年龄的平均数为:
27.5×0.02×5+32.5×0.02×5+37.5×0.08×5+42.5×0.06×5+47.5×0.02×5=38.5,
∵[25,35)上的频率为(0.02+0.02)×5=0.2,[35,40)上的频率为0.08×5=0.4,
∴中位数为:35+$\frac{0.5-0.2}{0.4}×5$=38.75.
和中位数
(3)因为第1,2,3组共有50+50+200=300人,
利用分层抽样在300名学生中抽取6名学生,每组抽取的人数分别为:
第1组的人数为6×$\frac{50}{300}$=1,
第2组的人数为6×$\frac{50}{300}$=1,
第3组的人数为6×$\frac{200}{300}$=4,
所以第1,2,3组分别抽取1人,1人,4人.
(3)设第1组的1位同学为A,第2组的1位同学为B,
第3组的4位同学为C1,C2,C3,C4,
则从六位同学中抽两位同学有:
(A,B),(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),(B,C2),(B,C3),
(B,C4),(C1,C2),(C1,C3),(C1,C4),(C2,C3),(C2,C4),(C3,C4),共15种可能.
其中恰有1人年龄在第3组有8种可能,
所以恰有1人年龄在第3组的概率为P=$\frac{8}{15}$.
点评 本题考查频率分布直方图的读法、分层抽样以及随机事件的概率等基础知识,考查学生的分析能力和计算能力,是中档题,解题时要认真审题,注意频率分布直方图的合理运用.

 名校课堂系列答案
名校课堂系列答案| 得禽流感 | 不得禽流感 | 总计 | |
| 服药 | 5 | 20 | 25 |
| 不服药 | 15 | 10 | 25 |
| 总计 | 20 | 30 | 50 |
(2)在服药后得禽流感的鸭子中,有2只母鸭,3只公鸭,在这5只中随机抽取3只再进行研究,求至少抽到1只母鸭的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
| A. | $2\sqrt{2}$ | B. | $\frac{4}{{\sqrt{{m^2}+{n^2}}}}$ | C. | $\frac{2}{{\sqrt{{m^2}+{n^2}}}}+\sqrt{2}$ | D. | 不确定 |
| A. | a<-2 | B. | a>-2 | C. | a>-$\frac{1}{2}$ | D. | a<-$\frac{1}{2}$ |




