题目内容
13．已知曲线y=$\frac{{x}^{2}}{2}$-3lnx的一条切线的与直线x+2y+10=0垂直，则切点的横坐标为（ ）| A． | $\frac{1}{3}$ | B． | 2 | C． | 1 | D． | 3 |
分析 设出切点坐标，求出原函数的导函数，结合切线与直线x+2y+10=0垂直，可得关于切点横坐标的方程，求解得答案．
解答 解：设切点坐标为（x0，y0），且x0＞0，
由y′=x-$\frac{3}{x}$，得k=x0-$\frac{3}{{x}_{0}}$，
∵切线与直线x+2y+10=0垂直，
∴x0-$\frac{3}{{x}_{0}}$=2，解得x0=3或x0=-1（舍）．
故选：D．
点评 本题考查利用导数研究过曲线上某点处的切线方程，关键是明确函数在某点处的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
3．
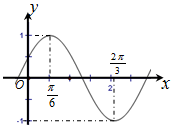已知函数f（x）=Asin（ωx+φ）（A＞0，?＞0，|φ|＜$\frac{π}{2}$）的简图如下，则A，ω，φ分别为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，?＞0，|φ|＜$\frac{π}{2}$）的简图如下，则A，ω，φ分别为（ ）| A． | 1，2，-$\frac{π}{3}$ | B． | 1，$\frac{1}{2}$，-$\frac{π}{3}$ | C． | 1，2，$\frac{π}{6}$ | D． | 1，$\frac{1}{2}$，$\frac{π}{6}$ |
1．已知方程$\frac{x^2}{m-1}+\frac{y^2}{4-m}=1$表示焦点在x轴上的双曲线的一个充分不必要条件是（ ）
| A． | （4，+∞） | B． | （5，+∞） | C． | $（1，\frac{5}{2}）$ | D． | （1，2） |
8．若变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤8\\ 2y-x≤4\end{array}\right.$，且z=5y-x的最大值为a，最小值为b，则a-b的值是（ ）
| A． | 16 | B． | 24 | C． | 30 | D． | 48 |
5．已知两点A（1，2）．B（2，1）在直线mx-y+1=0的异侧，则实数m的取值范围为（ ）
| A． | （-∞，0） | B． | （1，+∞） | C． | （0，1） | D． | （-∞，0）∪（1，+∞） |
2．为了考察某种药物预防禽流感的效果，某研究中心选了50只鸭子做实验，统计结果如下：
（1）能有多大的把握认为药物有效？
（2）在服药后得禽流感的鸭子中，有2只母鸭，3只公鸭，在这5只中随机抽取3只再进行研究，求至少抽到1只母鸭的概率．
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
临界值表：
| 得禽流感 | 不得禽流感 | 总计 | |
| 服药 | 5 | 20 | 25 |
| 不服药 | 15 | 10 | 25 |
| 总计 | 20 | 30 | 50 |
（2）在服药后得禽流感的鸭子中，有2只母鸭，3只公鸭，在这5只中随机抽取3只再进行研究，求至少抽到1只母鸭的概率．
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
临界值表：
| P（K2≥k0） | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |