题目内容
5.在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为2$\sqrt{3}$,$\sqrt{3}$c=2asinC,a=2$\sqrt{3}$,则b+c=6.分析 由$\sqrt{3}$c=2asinC,利用正弦定理,可得2sinAsinC=$\sqrt{3}$sinC,求角A,利用ABC的面积,再利用余弦定理,即可求b+c的大小.
解答 解:由$\sqrt{3}$c=2asinC,得2sinAsinC=$\sqrt{3}$sinC,
∵sinC≠0,∴sinA=$\frac{\sqrt{3}}{2}$
又∵△ABC是锐角△,
∴A=$\frac{π}{3}$,
∵△ABC的面积为2$\sqrt{3}$,
∴$\frac{1}{2}bc•\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴bc=8,
∵12=b2+c2-bc,
∴b2+c2=20,
∴(b+c)2=36
∴b+c=6,
故答案为6.
点评 本题考查正弦定理、余弦定理的运用,考查学生的计算能力,正确运用正弦定理、余弦定理是关键.

练习册系列答案
相关题目
16.定义为n个正数p1,p2,p3…pn的“均倒数”,若已知数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,又${b_n}=\frac{{{a_n}+1}}{4}$,则$\frac{1}{{{b_1}{b_2}}}+\frac{1}{{{b_2}{b_3}}}+\frac{1}{{{b_3}{b_4}}}+$…$+\frac{1}{{{b_{2015}}{b_{2016}}}}$=( )
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
13.某大型汽车城为了了解销售单价(单位:万元)在[8,20]内的轿车的销售情况,从2016年上半年已经销售的轿车中随机抽取100辆,按其销售单价分成6组,制成如下的频数分布表.
已知样本中销售单价在[14,16)内的轿车数是销售单价在[18,20]内的轿车数的2倍.
(1)用分层抽样的方法从单价在[8,10),[10,12)和[18,20]内的轿车中共抽取6辆,求销售单价在[18,20]内的轿车数;
(2)在(1)中抽出的6辆轿车中任取2辆,求至少有1辆轿车的销售单价在[18,20]内的概率.
| 销售单价/万元 | [8,10) | [10,12) | [12,14) | [14,16) | [16,18) | [18,20] |
| 频数/辆 | 5 | 10 | 20 | a | 20 | b |
(1)用分层抽样的方法从单价在[8,10),[10,12)和[18,20]内的轿车中共抽取6辆,求销售单价在[18,20]内的轿车数;
(2)在(1)中抽出的6辆轿车中任取2辆,求至少有1辆轿车的销售单价在[18,20]内的概率.
20.设{an}是首项大于零的等比数列,则“a12<a22”是“数列{an}为递增数列”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.某地区2011年至2015年农村居民家庭人均纯收入y(单位:万元)的数据如表:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x}•\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}}\\{\hat a=\overline y-\hat b\overline x}\end{array}}\right.$.
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
(2)利用(1)中的回归方程,分析2011年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x}•\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}}\\{\hat a=\overline y-\hat b\overline x}\end{array}}\right.$.
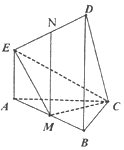 如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.
如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.