题目内容
8. 16.如图所示,在正方形ABCD中,已知|$\overrightarrow{AB}$|=2,若N为正方形内(含边界)任意一点,则$\overrightarrow{AB}$•$\overrightarrow{AN}$的最大值是4.
16.如图所示,在正方形ABCD中,已知|$\overrightarrow{AB}$|=2,若N为正方形内(含边界)任意一点,则$\overrightarrow{AB}$•$\overrightarrow{AN}$的最大值是4.
分析 在平面内建立合适的坐标系,将向量的数量积用坐标表示,构造函数,利用求函数的最值来解决问题.
解答 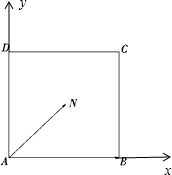 解:以A为坐标原点,以AB方向为x轴正方向,
解:以A为坐标原点,以AB方向为x轴正方向,
以AD方向为y轴负方向建立坐标系,
∵正方形ABCD的边长为2,∴$\overrightarrow{AB}$=(2,0),
N为正方形内(含边界)一点,设N(x,y),
则0≤x≤2,0≤y≤2,$\overrightarrow{AN}$=(x,y),则$\overrightarrow{AB}•\overrightarrow{AN}$=2x≤4,
当N在BC上时取得最大值4,
故答案是:4.
点评 向量的主要功能就是数形结合,将几何问题转化为代数问题,但关键是建立合适的坐标系,将向量用坐标表示,再将数量积运算转化为方程或函数问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
18.考察下列每组对象哪几组能够成集合?( )
(1)比较小的数
(2)不大于10的偶数
(3)所有三角形
(4)高个子男生.
(1)比较小的数
(2)不大于10的偶数
(3)所有三角形
(4)高个子男生.
| A. | (1)(4) | B. | (2)(3) | C. | (2) | D. | (3) |
16.从集合{0,1,2,3,4,5}中任取两个互不相等的数a,b组成复数a+bi,其中虚数有( )个.
| A. | 36 | B. | 30 | C. | 25 | D. | 20 |
13.某样本中共有5个个体,其中四个值分别为0,1,2,3,第五个值丢失,但该样本的平均值为1,则样本方差为( )
| A. | 2 | B. | $\frac{6}{5}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{30}}}{5}$ |