题目内容
7.已知函数$f(x)=xcosx-\frac{a}{x}sinx-sinx,x∈({-kπ,0})∪({0,kπ})$(其中k为正整数,a∈R,a≠0),则f(x)的零点个数为( )| A. | 2k-2 | B. | 2k | C. | 2k-1 | D. | 与a有关 |
分析 函数f(x)零点的个数等于方程xcosx-sinx=$\frac{a}{x}$sinx,x∈(-kπ,0)∪(0,kπ)解的个数;
设y1=xcosx-sinx,y2=$\frac{a}{x}$sinx,利用导数研究两个函数的单调性与交点个数,即可求出答案.
解答 解:函数f(x)=xcosx-$\frac{a}{x}$sinx-sinx,x∈(-kπ,0)∪(0,kπ)的零点的个数
等于方程xcosx-sinx=$\frac{a}{x}$sinx,x∈(-kπ,0)∪(0,kπ)解的个数;
设y1=xcosx-sinx,y2=$\frac{a}{x}$sinx,
∵y1′=-xsinx,∴y1=xcosx-sinx
在…,(-5π,-4π),(-3π,-2π),(-π,0),(0,π),(2π,3π),(4π,5π),…上单调递减;
在…,(-4π,-3π),(-2π,-π),(π,2π),(3π,4π),…上单调递增;
如图中实线所示;
y2′=a$\frac{xcosx-sinx}{{x}^{2}}$,由y1=xcosx-sinx的图象可得:
a>0时,y2=$\frac{a}{x}$sinx的图象,如图中虚线所示;
则函数f(x)共有2k-1个零点;
由函数图象的对称性可得,
当a<0时,函数f(x)零点个数仍为2k-1个.
故选:C.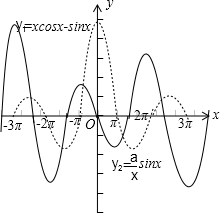
点评 本题考查了三角函数的图象与性质的应用问题,也考查了函数零点与方程根的应用问题,是难题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
15.两位同学约定下午5:30~6:00在图书馆见面,且他们在5:30~6:00之间到达的时刻是等可能的,先到的同学须等待,15分钟后还未见面便离开,则两位同学能够见面的概率是( )
| A. | $\frac{11}{36}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
12.设i为虚数单位,则$\frac{3-i}{i}$=( )
| A. | -1-3i | B. | 1-3i | C. | -1+3i | D. | 1+3i |
17.已知x=log52,y=ln2,z=${2}^{\frac{1}{2}}$,则下列结论正确的是( )
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
 ,那么这组数据的方差S2可能的最大值是$\frac{164}{5}$.
,那么这组数据的方差S2可能的最大值是$\frac{164}{5}$.