题目内容
4.已知集合A={1,2,3},B={x∈Z|(x+2)(x-3)<0},则A∪B( )| A. | {1} | B. | {-1,0,1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
分析 先分别求出集合A,B,由此利用并集定义能求出A∪B.
解答 解:∵集合A={1,2,3},
B={x∈Z|(x+2)(x-3)<0}={-1,0,1,2,},
∴A∪B={-1,01,1,2,3}.
故选:B.
点评 本题考查并集的求法,是基础题,解题时要认真审题,注意并集定义的合理运用.

练习册系列答案
相关题目
15.两位同学约定下午5:30~6:00在图书馆见面,且他们在5:30~6:00之间到达的时刻是等可能的,先到的同学须等待,15分钟后还未见面便离开,则两位同学能够见面的概率是( )
| A. | $\frac{11}{36}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
12.设i为虚数单位,则$\frac{3-i}{i}$=( )
| A. | -1-3i | B. | 1-3i | C. | -1+3i | D. | 1+3i |
9.已知实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x+y≤0}\\{2x+y+2≤0}\end{array}\right.$且ax-y+1-a=0,则实数a的取值范围是( )
| A. | [-$\frac{1}{3}$,1) | B. | [-1,$\frac{1}{2}$] | C. | (-1,$\frac{1}{2}$] | D. | [-$\frac{1}{3}$,$\frac{1}{2}$] |
14.已知棱长为$\sqrt{6}$的正四面体ABCD(四个面都是正三角形),在侧棱AB上任取一点P(与A,B都不重合),若点P到平面BCD及平面ACD的距离分别为a,b,则$\frac{4}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
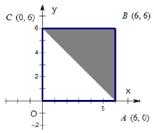 如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).
如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).