题目内容
5.已知不等式x2-ax+a-2>0的解集为(-∞,x1)∪(x2+∞),其中x1<0<x2,则${x_1}+{x_2}+\frac{2}{x_1}+\frac{2}{x_2}$的最大值为( )| A. | $\frac{3}{2}$ | B. | 0 | C. | 2 | D. | $-\frac{3}{2}$ |
分析 根据不等式x2-ax+a-2>0的解集,得出x1x2=a-2<0,求出${x_1}+{x_2}+\frac{2}{x_1}+\frac{2}{x_2}$=(a-2)+$\frac{4}{a-2}$+4;利用基本不等式求出它的最大值即可.
解答 解:不等式x2-ax+a-2>0的解集为(-∞,x1)∪(x2,+∞),其中x1<0<x2,
∴x1x2=a-2<0,
∴${x_1}+{x_2}+\frac{2}{x_1}+\frac{2}{x_2}$=(x1+x2)+$\frac{2({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$
=a+$\frac{2a}{a-2}$
=a+$\frac{2a-4+4}{a-2}$
=a+2+$\frac{4}{a-2}$
=(a-2)+$\frac{4}{a-2}$+4;
又a-2<0,∴-(a-2)>0,
∴-(a+2)-$\frac{4}{a-2}$≥2$\sqrt{-(a-2)•\frac{-4}{a-2}}$=4,
当且仅当-(a-2)=-$\frac{4}{a-2}$,即a=0时,取“=”;
∴(a-2)+$\frac{4}{a-2}$+4≤-4+4=0,
即${x_1}+{x_2}+\frac{2}{x_1}+\frac{2}{x_2}$的最大值为0.
故选:B.
点评 本题考查一元二次不等式的解法与应用问题,也考查了基本不等式的应用问题,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.两位同学约定下午5:30~6:00在图书馆见面,且他们在5:30~6:00之间到达的时刻是等可能的,先到的同学须等待,15分钟后还未见面便离开,则两位同学能够见面的概率是( )
| A. | $\frac{11}{36}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
20.已知向量$\overrightarrow{a}$=(0,1,1),$\overrightarrow{b}$=(1,2,0),则同时与$\overrightarrow{a}$,$\overrightarrow{b}$垂直的单位向量$\overrightarrow{e}$=( )
| A. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$ | B. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | ||
| C. | $(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ | D. | $(-\frac{{\sqrt{6}}}{3},\frac{{\sqrt{6}}}{6},-\frac{{\sqrt{6}}}{6})$或$(\frac{{\sqrt{6}}}{3},-\frac{{\sqrt{6}}}{6},\frac{{\sqrt{6}}}{6})$ |
17.已知x=log52,y=ln2,z=${2}^{\frac{1}{2}}$,则下列结论正确的是( )
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
14.已知棱长为$\sqrt{6}$的正四面体ABCD(四个面都是正三角形),在侧棱AB上任取一点P(与A,B都不重合),若点P到平面BCD及平面ACD的距离分别为a,b,则$\frac{4}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
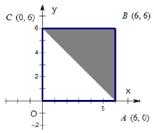 如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).
如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).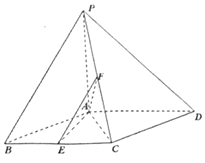 已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.
已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.