题目内容
设函数f(x)=ax2+bx+c(a、b、c∈R,且a>0),若a=1,又知x1,x2是方程f(x)=0的两个根,且x1,x2∈(m,m+1),其中m∈R,求f(m)f(m+1)的最大值.
考点:二次函数的性质
专题:函数的性质及应用
分析:设f(x)=(x-x1)(x-x2),x1,x2∈(m,m+1),得到f(m)•f(m+1)=(m-x1)(m-x2)(m+1-x1)(m+1-x2)=[(x1-m)(m+1-x1)][(x2-m)(m+1-x2],再利用基本不等式求最值.
解答:
解:不妨设f(x)=(x-x1)(x-x2),x1,x2∈(m,m+1),
由m-x1<0,m-x2<0,m+1-x1>0,m+1-x2>0,
∴f(m)•f(m+1)=(m-x1)(m-x2)(m+1-x1)(m+1-x2)
=[(x1-m)(m+1-x1)][(x2-m)(m+1-x2]
≤(
)2•(
)2
=
,
当且仅当x1=x2=m+
时取等号,
∴f(m)f(m+1)的最大值为
.
由m-x1<0,m-x2<0,m+1-x1>0,m+1-x2>0,
∴f(m)•f(m+1)=(m-x1)(m-x2)(m+1-x1)(m+1-x2)
=[(x1-m)(m+1-x1)][(x2-m)(m+1-x2]
≤(
| x1-m+m+1-x1 |
| 2 |
| x2-m+m+1x2 |
| 2 |
=
| 1 |
| 16 |
当且仅当x1=x2=m+
| 1 |
| 2 |
∴f(m)f(m+1)的最大值为
| 1 |
| 16 |
点评:本题属于二次函数的性质问题,在求解过程中注意基本不等式的应用问题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
设集合M={y|y=2sinx,-2≤x≤2},N={x|lgx>0},则M∩N=( )
| A、{x|1<x≤5} |
| B、{x|-1<x≤0} |
| C、{x|-2<x≤0} |
| D、{x|1<x≤2} |
已知集合M={x∈Z|log3x≤1},N={x∈Z|x2-2x<0},则( )
| A、M=N | B、M∩N=∅ |
| C、M∩N=R | D、M?N |
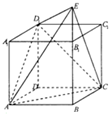 如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,E为BB1延长线上的一点且满足
如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,E为BB1延长线上的一点且满足