题目内容
已知点A(x,y)和点B(-4,y),以AB为直径的圆经过坐标原点O.
(1)求点A的轨迹C的方程;
(2)过点P(4,0)的直线l交轨迹C于D,E两点,判断△DOE的形状,并证明你的结论.
(1)求点A的轨迹C的方程;
(2)过点P(4,0)的直线l交轨迹C于D,E两点,判断△DOE的形状,并证明你的结论.
考点:轨迹方程,直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)以AB为直径的圆经过坐标原点O,则OA⊥OB,由此可求点A的轨迹C的方程;
(2)△DOE是直角三角形.设l:x=my+4,代入y2=4x,证明
•
=0,即可得出结论.
(2)△DOE是直角三角形.设l:x=my+4,代入y2=4x,证明
| OD |
| OE |
解答:
解:(1)∵以AB为直径的圆经过坐标原点O,
∴OA⊥OB,
∴(x,y)•(-4,y)=0,
∴-4x+y2=0,
∴y2=4x;
(2)△DOE是直角三角形.
设l:x=my+4,代入y2=4x,可得y2-4my-16=0,
设D(x1,y1),E(x2,y2),则y1+y2=4my,y1y2=-16,
∴
•
=x1x2+y1y2=
-16=0,
∴OD⊥OE,
∴△DOE是直角三角形.
∴OA⊥OB,
∴(x,y)•(-4,y)=0,
∴-4x+y2=0,
∴y2=4x;
(2)△DOE是直角三角形.
设l:x=my+4,代入y2=4x,可得y2-4my-16=0,
设D(x1,y1),E(x2,y2),则y1+y2=4my,y1y2=-16,
∴
| OD |
| OE |
| y12y22 |
| 16 |
∴OD⊥OE,
∴△DOE是直角三角形.
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查向量知识的运用,属于中档题.

练习册系列答案
相关题目
函数y=
的值域为( )
| 2sinx-3 |
| sinx-1 |
| A、(-∞,-2] | ||
B、(-∞,
| ||
| C、(-2,+∞) | ||
D、[
|
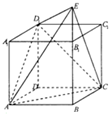 如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,E为BB1延长线上的一点且满足
如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,E为BB1延长线上的一点且满足 已知函数f(x)=2sin(ωx+φ)(其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是
已知函数f(x)=2sin(ωx+φ)(其中x∈R,ω>0,-π<φ<π)的部分图象如图所示,则函数f(x)的解析式是