题目内容
若(1-2x)2014=a0+a1x+a2x2+…+a2014x2014,则(a0+a1)+(a0+a2)+…+(a0+a2014)= .
考点:二项式系数的性质
专题:二项式定理
分析:在所给的等式中,令x=0求得a0=1,再令x=1,可得a0+a1+a2+…+a2014 =1,而要求的式子即[a0+a1+a2+…+a2014 ]+2013a0,从而求得要求式子的值.
解答:
解:在(1-2x)2014=a0+a1x+a2x2+…+a2014x2014 中,
令x=0可得a0=1.
再令x=1,可得a0+a1+a2+…+a2014 =1,
∴(a0+a1)+(a0+a2)+…+(a0+a2014)=[a0+a1+a2+…+a2014 ]+2013a0=1+2013=2014,
故答案为:2014.
令x=0可得a0=1.
再令x=1,可得a0+a1+a2+…+a2014 =1,
∴(a0+a1)+(a0+a2)+…+(a0+a2014)=[a0+a1+a2+…+a2014 ]+2013a0=1+2013=2014,
故答案为:2014.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知“有序整数对”按如下规律排列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1)…,则第62个“有序整数对”是( )
| A、(7,5) |
| B、(8,4) |
| C、(9,3) |
| D、(10,2) |
下列结论正确的是( )
①相关关系是一种非确定性关系;
②任一组数据都有回归方程;
③散点图能直观地反映数据的相关程度.
①相关关系是一种非确定性关系;
②任一组数据都有回归方程;
③散点图能直观地反映数据的相关程度.
| A、①② | B、②③ | C、①③ | D、①②③ |
若a、b为实数,则“0<ab<1”是“0<a<
”的( )
| 1 |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
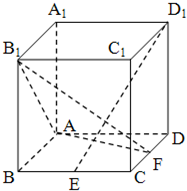 如图,在正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.当
如图,在正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.当