题目内容
 如图,已知四棱锥P-ABCD的底面为菱形,PA⊥面ABCD,且PA=AB,∠BAD=60°,E、F分别是PA、BC的中点.
如图,已知四棱锥P-ABCD的底面为菱形,PA⊥面ABCD,且PA=AB,∠BAD=60°,E、F分别是PA、BC的中点.(Ⅰ)求证:BE∥平面PDF;
(Ⅱ)过BD作一平面交棱PC于点M,若二面角M-BD-C的大小为60°,求
| CM |
| MP |
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)取PD的中点G,连结EG、FG,证明四边形EGFB是平行四边形,可得BE∥FG,即可证明BE∥平面PDF;
(Ⅱ)连结AC交BD于O,连结OM,证明∠MOC就是二面角M-BD-C的平面角,求出CM,即可求
的值.
(Ⅱ)连结AC交BD于O,连结OM,证明∠MOC就是二面角M-BD-C的平面角,求出CM,即可求
| CM |
| MP |
解答:
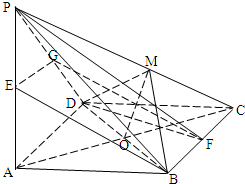 (Ⅰ)证明:取PD的中点G,连结EG、FG,
(Ⅰ)证明:取PD的中点G,连结EG、FG,
因为E是PA的中点,所以EG∥AD,且EG=
AD,
又F是菱形ABCD边BC 的中点,
所以BF∥AD,且BF=
AD,
所以EG∥BC,且EG=BC,
所以四边形EGFB是平行四边形,
所以BE∥FG,…(5分)
而FG?平面,BE?平面PDF,…(6分)
所以BE∥平面PDF.…(7分)
(Ⅱ)解:连结AC交BD于O,连结OM,
因为PA⊥面ABCD,所以PA⊥BD,
又BD⊥AC,且PA∩AC=A,
所以BD⊥平面PAC,…(10分)
从而OM⊥BD,OCBD,
所以∠MOC就是二面角M-BD-C的平面角,∠MOC=60°,…(12分)
设AB=1,因为PA=AB,∠BAD=60°,
所以PA=1,AC=
,PC=2,∠PCA=30°,
所以∠OMC=90°,
在Rt△OCM中,CM=
cos30°=
,…(14分)
所以
=
=
…(15分)
 (Ⅰ)证明:取PD的中点G,连结EG、FG,
(Ⅰ)证明:取PD的中点G,连结EG、FG,因为E是PA的中点,所以EG∥AD,且EG=
| 1 |
| 2 |
又F是菱形ABCD边BC 的中点,
所以BF∥AD,且BF=
| 1 |
| 2 |
所以EG∥BC,且EG=BC,
所以四边形EGFB是平行四边形,
所以BE∥FG,…(5分)
而FG?平面,BE?平面PDF,…(6分)
所以BE∥平面PDF.…(7分)
(Ⅱ)解:连结AC交BD于O,连结OM,
因为PA⊥面ABCD,所以PA⊥BD,
又BD⊥AC,且PA∩AC=A,
所以BD⊥平面PAC,…(10分)
从而OM⊥BD,OCBD,
所以∠MOC就是二面角M-BD-C的平面角,∠MOC=60°,…(12分)
设AB=1,因为PA=AB,∠BAD=60°,
所以PA=1,AC=
| 3 |
所以∠OMC=90°,
在Rt△OCM中,CM=
| ||
| 2 |
| 3 |
| 4 |
所以
| CM |
| MP |
| ||
2-
|
| 3 |
| 5 |
点评:本题考查线面平行,考查面面角,考查学生分析解决问题的能力,正确运用线面平行的判定定理是关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

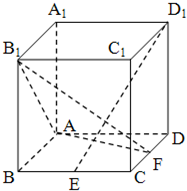 如图,在正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.当
如图,在正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.当