题目内容
△ABC中,BC=1,AB=
,AC=
,点P是△ABC的外接圆上的一个动点,则
•
的最大值为 .
| 3 |
| 6 |
| BP |
| BC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,
•
=|
| |
|cos∠PBC=|
|cos∠PBC.设OP⊙O的半径,则 当OP∥BC且同向时,则
•
取得最大值.再利用正弦定理和余弦定理即可得出、垂径定理即可得出.
| BP |
| BC |
| BP |
| BC |
| BP |
| BP |
| BC |
解答:
解:如图所示,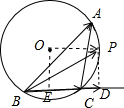
•
=|
| |
|cos∠PBC=|
|cos∠PBC.
设OP为⊙O的半径,则 当OP∥BC且同向时,向量
在
方向上的投影最大,则
•
取得最大值.
由余弦定理可得:cosA=
=
,∴sinA=
.
∴2R=
=3.
∴|
|cos∠PBC=|BD|=
|BC|+R=2.
∴
•
取得最大值为2.
故答案为:2.

| BP |
| BC |
| BP |
| BC |
| BP |
设OP为⊙O的半径,则 当OP∥BC且同向时,向量
| BP |
| BC |
| BP |
| BC |
由余弦定理可得:cosA=
| 3+6-1 | ||||
2×
|
2
| ||
| 3 |
| 1 |
| 3 |
∴2R=
| BC |
| sinA |
∴|
| BP |
| 1 |
| 2 |
∴
| BP |
| BC |
故答案为:2.
点评:本题考查了向量的数量积运算、向量的投影、正弦定理和余弦定理、垂径定理等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
下列结论正确的是( )
①相关关系是一种非确定性关系;
②任一组数据都有回归方程;
③散点图能直观地反映数据的相关程度.
①相关关系是一种非确定性关系;
②任一组数据都有回归方程;
③散点图能直观地反映数据的相关程度.
| A、①② | B、②③ | C、①③ | D、①②③ |
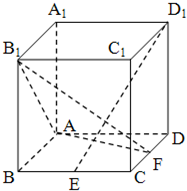 如图,在正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.当
如图,在正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.当