题目内容
8.在三棱锥P-ABC中,底面ABC是等腰三角形,∠BAC=120°,BC=2,PA⊥平面ABC,若三棱锥P-ABC的外接球的表面积为8π,则该三棱锥的体积为( )| A. | $\frac{\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{2}}{9}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{9}$ |
分析 由题意画出图形,设出底面三角形的外心G,找出三棱锥P-ABC的外接球的球心O,通过求解直角三角形得到三棱锥的高,则答案可求.
解答 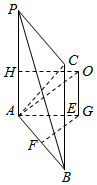 解:如图
解:如图
取BC中点为E,连接AE,
∵底面ABC是等腰三角形,∠BAC=120°,BC=2,
∴△ABC的外心G在AE上,设为G,取AB中点F,连接GF,
在Rt△AEB中,由BE=1,∠BAE=60°,得AF=$\frac{1}{2}AB$=$\frac{1}{2}×\frac{1}{sin60°}=\frac{\sqrt{3}}{3}$,
又在Rt△AFG中,得$AG=\frac{AF}{cos60°}=\frac{2\sqrt{3}}{3}$,
过G作PA的平行线与PA的中垂线HO交于O,
则O为三棱锥P-ABC的外接球的球心,即R=OA,
由4πR2=8π,得R=$\sqrt{2}$,
∵PA⊥平面ABC,∴OG⊥AG,
在Rt△AGO中,求得OG=$\sqrt{{R}^{2}-A{G}^{2}}=\sqrt{2-\frac{4}{3}}=\frac{\sqrt{6}}{3}$,
∴三棱锥P-ABC的高PA=2OG=$\frac{2\sqrt{6}}{3}$,
则三棱锥的体积为V=$\frac{1}{3}×\frac{1}{2}×2×\frac{\sqrt{3}}{3}×\frac{2\sqrt{6}}{3}=\frac{2\sqrt{2}}{9}$.
故选:B.
点评 本题考查棱柱、棱锥、棱台的体积,考查空间想象能力和思维能力,考查计算能力,是中档题.

练习册系列答案
相关题目
19.设复数z满足(z-1)(1+i)=2(i为虚数单位),则|z|=( )
| A. | 1 | B. | 5 | C. | $\sqrt{5}$ | D. | $\sqrt{13}$ |
3.设直线l与平面α平行,直线m在平面α上,那么( )
| A. | 直线l平行于直线m | B. | 直线l与直线m异面 | ||
| C. | 直线l与直线m没有公共点 | D. | 直线l与直线m不垂直 |
18.已知tanα=1,那么$\frac{sinα-2cosα}{3sinα+cosα}$=( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |