题目内容
定义:如果函数y=f(x)在区间[a,b]上存在x1,x2(a<x1<x2<b),满足f′(x1)=
,f′(x2)=
,则称函数y=f(x)在区间[a,b]上的一个双中值函数,已知函数f(x)=
x3-x2+a是区间[0,a]上的双中值函数,则实数a的取值范围是( )
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
| 1 |
| 3 |
A、(0,
| ||
B、(
| ||
C、(
| ||
| D、(1,3) |
考点:利用导数研究函数的单调性,函数单调性的判断与证明
专题:新定义
分析:根据题目给出的定义可得f′(x1)=f′(x2)=
=
=
a2-a,即方程x2-2x=
a2-a在区间(0,a)有两个解,利用二次函数的性质可知实数a的取值范围是(
,3).
| f(a)-f(0) |
| a |
| ||
| a |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
解答:
解:由题意可知,
在区间[0,a]存在x1,x2(a<x1<x2<b),
满足f′(x1)=f′(x2)=
=
=
a2-a,
∵f(x)=
x3-x2+a,
∴f′(x)=x2-2x,
∴方程x2-2x=
a2-a在区间(0,a)有两个解.
令g(x)=x2-2x-
a2+a,(0<x<a)
则
,
解得,
<a<3.
∴实数a的取值范围是(
,3).
故选:B.
在区间[0,a]存在x1,x2(a<x1<x2<b),
满足f′(x1)=f′(x2)=
| f(a)-f(0) |
| a |
| ||
| a |
| 1 |
| 3 |
∵f(x)=
| 1 |
| 3 |
∴f′(x)=x2-2x,
∴方程x2-2x=
| 1 |
| 3 |
令g(x)=x2-2x-
| 1 |
| 3 |
则
|
解得,
| 3 |
| 2 |
∴实数a的取值范围是(
| 3 |
| 2 |
故选:B.
点评:本题主要考查了导数的几何意义,二次函数的性质与方程根的关系,属于中档题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
复数z=1+i,则
+
对应的点所在的象限为( )
| 1 |
| z |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,点M是BC中点.若∠A=120°,
•
=-
,则|
|的最小值是( )
| AB |
| AC |
| 1 |
| 2 |
| AM |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
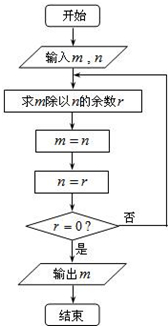 如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )
如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )| A、2010 | B、1541 |
| C、134 | D、67 |
等差数列x1,x2,x3…x9的公差为1,随机变量ξ等可能的取值x1,x2,x3…x9,则方差D(ξ)为( )
A、
| ||
B、
| ||
C、
| ||
D、
|