题目内容
△ABC中A,B,C的对边分别是a,b,c,若
=
,(b+c+a)(b+c-a)=3bc,则△ABC的形状为( )
| sinA |
| sinB |
| a |
| c |
| A、等边三角形 |
| B、等腰非等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |
考点:正弦定理
专题:解三角形
分析:把(b+c+a)(b+c-a)=3bc整理课求得b2+c2-a2和bc的关系式,代入余弦定理中可求得cosA的值,进而取得A,同时利用正弦定理和
=
整理后可知b=c,最后可判断出三角形的形状.
| sinA |
| sinB |
| a |
| c |
解答:
解:∵(b+c+a)(b+c-a)=3bc,
∴(b+c)2-a2=3bc,
∴b2+c2+2bc-a2=3bc,
∴b2+c2-a2=bc,
由余弦定理得:cosA=
=
,A∈(0,π),
∴A=
,
∵△ABC中,由正弦定理得:
=
,
∴
=
,又
=
,
∴
=
,
∴b=c,
综合可知三角形为等边三角形.
故选:A.
∴(b+c)2-a2=3bc,
∴b2+c2+2bc-a2=3bc,
∴b2+c2-a2=bc,
由余弦定理得:cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
∴A=
| π |
| 3 |
∵△ABC中,由正弦定理得:
| a |
| sinA |
| b |
| sinB |
∴
| sinA |
| sinB |
| a |
| b |
| sinA |
| sinB |
| a |
| c |
∴
| a |
| b |
| a |
| c |
∴b=c,
综合可知三角形为等边三角形.
故选:A.
点评:本题主要考查了正弦定理和余弦定理的应.解题的关键是利用正弦定理和余弦定理完成角和边的问题的转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
知向量
、
、
中任意二个都不共线,但
+
与
共线,且
+
与
共线,则向量
+
+
=( )
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| a |
| a |
| b |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sin2α=
,则cos2(α-
)=( )
| 1 |
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
复数z=(m-1)(m-8)+
ilog2m(m∈R)是纯虚数,则
=( )
| 1 |
| 3 |
| 1 |
| 1-z |
| A、1+i | ||||
| B、1-i | ||||
C、
| ||||
D、
|
不等式|x-2|<1的解集为( )
| A、[1,3] |
| B、(1,3) |
| C、[-3,-1] |
| D、(-3,-1) |
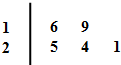 学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )
学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )| A、21和10.8 |
| B、24和10.8 |
| C、25和9.2 |
| D、5和9.2 |
执行如图所示的程序框图,如输入的p=20,则输出的n的值是( )


| A、3 | B、4 | C、5 | D、6 |
已知某物体的运动曲线方程为:S=2t2-3t-1,则该物体在t=3时的速度为( )
| A、8 | B、9 | C、10 | D、11 |