题目内容
10.已知抛物线y=ax2(a>0)的焦点到准线的距离为2,则a=( )| A. | 4 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 将抛物线方程转化成标准方程,则2p=$\frac{1}{a}$,由焦点到准线的距离d=p=$\frac{1}{2a}$=2,即可求得a的值.
解答 解:抛物线x2=$\frac{1}{a}$y(a>0),焦点在y轴的正半轴,即2p=$\frac{1}{a}$,
由焦点到准线的距离d=p=$\frac{1}{2a}$=2,
则a=$\frac{1}{4}$,
故选C.
点评 本题考查抛物线的标准方程,考查转化思想,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
8.已知曲线C1:y2=tx (y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+l-1也相切,则t的值为( )
| A. | 4e2 | B. | 4e | C. | $\frac{e^x}{4}$ | D. | $\frac{e}{4}$ |
15.一个口袋中装有2个白球和3个黑球,这5个球除颜色外完全相同,从中摸出2个球,则这2个球颜色相同的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
2.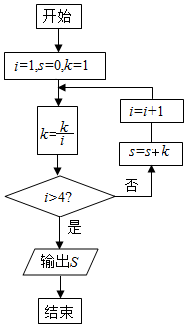 阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
 阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
阅读如图的程序框图,运行相应的程序,则输出的S的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{41}{24}$ | D. | $\frac{103}{60}$ |
19.已知定义在R上的奇函数f(x)满足:当x≥0时,f(x)=log2(x+m),则f(m-16)=( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
20.已知集合U={1,2,3,4,5,6,7},A={2,4,5,7},B={3,4,5}则(∁UA)∪B=( )
| A. | {3} | B. | {4,5} | C. | {1,3,4,5,6} | D. | {2,3,4,5,7} |
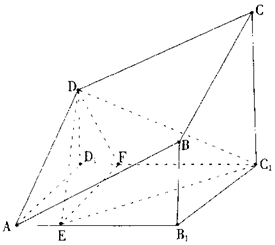 如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.
如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.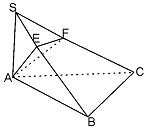 如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.