题目内容

函数f（x）=（m2-3）x m2-4m+3是幂函数，且在（0，+∞）上是减函数，则m=（　　）
A、2B、-2C、2或-2D、4
考点：幂函数的概念、解析式、定义域、值域
专题：函数的性质及应用
分析：根据函数f（x）是幂函数，且在（0，+∞）上的单调性，求出m的值．
解答： 解：∵函数f（x）=（m2-3）xm2-4m+3是幂函数，
∴m2-3=1，解得m=±2；
又∵f（x）在（0，+∞）上是减函数，
∴m2-4m+3＜0；
当m=2时，22-4×2+3=-1＜0，满足题意；
当m=-2时，（-2）2-4×（-2）+3=15＞0，不满足题意，舍去；
综上，m=2．
故选：A．
点评：本题考查了幂函数的定义、图象与性质的应用问题，解题时应熟记幂函数的定义与性质是什么．
练习册系列答案
相关题目
若关于x的二次函数f（x）=-x2+bx+c对一切实数x都有：f（2+x）=f（2-x）恒成立．
（1）求实数b的值；
（2）当a∈R时，判断f（
5
4
）与f（-a2-a+1）的大小，并说明理由．
已知曲线L的极坐标方程是ρ=2，正方形ABCD的顶点都在L上，且A、B、C、D依逆时针次序排列，点A的极坐标为（2，
π
3
），求其余各点B、C、D的极坐标．
△ABC的内角A，B，C所对的边分别为a，b，c．
（1）若A，B，C成等差数列，且AB=2，AC=2
3
，求△ABC的面积；
（2）若a，b，c成等比数列，且c=2a，求cos B的值．
盒中有4个相同的球，标号1，2，3，4．现从盒中随机摸一个，若摸出球上的数字是被摸球中最大的则留下，否则放回，则5次内（包括5次）把球摸完的概率为（　　）
A、
1
24
B、
23
288
C、
27
288
D、
35
288
已知符号函数sgnx=
1，x＞0
0，x=0
-1，x＜0
，则不等式（x2-2）•sgnx＞1的解集是（　　）
A、(-1，1)∪(
3
，+∞)
B、(-1，0)∪(
3
，+∞)
C、(-∞，
3
]∪(
3
，+∞)
D、(-∞，-
3
)∪(-1，1)∪(
3
，+∞)
已知不等式ax2-2ax-3＜0的解集是A
（1）若A=（-1，3）时，求a的值；
（2）若A等于实数集时，求实数a的范围．
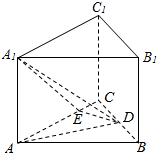如图，在正三棱柱ABC-A1B1C1中，AB=4，AA1=
7
，点D是BC的中点，点E在AC上，且DE⊥A1E．
（1）证明：平面A1DE⊥平面ACC1A1；
（2）求直线AD和平面A1DE所成角的正弦值．
设A、B、C、D是球面上的四点，AB、AC、AD两两互相垂直，且AB=5，AC=4，AD=
23
，则球的表面积为（　　）
A、36πB、64π
C、100πD、144π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网