题目内容
分设函数f(x)是定义在R上的函数,对任意实数m、n,都有f(m)•f(n)=f(m+n),且当x<0时,f(x)>1.
(1)证明当x>0时,0<f(x)<1;
(2)证明f(x)是R上的减函数;
(3)如果对任意实数x,有f(2ax-x2)•f(ax2-2x+4)<1恒成立,求实数a的取值范围.
(1)证明当x>0时,0<f(x)<1;
(2)证明f(x)是R上的减函数;
(3)如果对任意实数x,有f(2ax-x2)•f(ax2-2x+4)<1恒成立,求实数a的取值范围.
考点:函数恒成立问题,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)赋值法先求出f(0)的值,然后结合x<0时f(x)的范围;
(2)利用定义法,结合第一问的结果利用作商法比较f(x1)与f(x2)的大小;
(3)结合已知先将原式左边合并,将式子变成两个函数值的大小比较,再利用单调性列出不等式.
(2)利用定义法,结合第一问的结果利用作商法比较f(x1)与f(x2)的大小;
(3)结合已知先将原式左边合并,将式子变成两个函数值的大小比较,再利用单调性列出不等式.
解答:
解:(1)令m=0,n=-1,则f(0)f(-1)=f(-1),
∵f(-1)>0,∴f(0)=1,
再令m=x>0,n=-x则f(x)f(-x)=f(0)=1,∴f(x)=
,
∵-x<0,∴f(-x)>1∴0<
<1,
即当x>0时,0<f(x)<1
(2)设x1<x2,则f(x2)=f[(x2-x1)+x1]=f(x2-x1)f(x1),
∵x2-x1>0,∴0<f(x2-x1)<1,即0<
<1,∴f(x2)<f(x1),∴f(x)是R上的减函数,
(3)∵f(2ax-x2)•f(ax2-2x+4)<1,∴f(2ax-x2+ax2-2x+4)<f(0),
即f[(a-1)x2+2(a-1)x+4]<f(0),
∵f(x)是R上的减函数,∴(a-1)x2+2(a-1)x+4>0要恒成立.
当a=1时,不等式4>0恒成立.
当a>1时,则△=[2(a-1)]2-4(a-1)×4<0解得 1<x<5,∴1≤x<5.
∵f(-1)>0,∴f(0)=1,
再令m=x>0,n=-x则f(x)f(-x)=f(0)=1,∴f(x)=
| 1 |
| f(-x) |
∵-x<0,∴f(-x)>1∴0<
| 1 |
| f(-x) |
即当x>0时,0<f(x)<1
(2)设x1<x2,则f(x2)=f[(x2-x1)+x1]=f(x2-x1)f(x1),
∵x2-x1>0,∴0<f(x2-x1)<1,即0<
| f(x2) |
| f(x1) |
(3)∵f(2ax-x2)•f(ax2-2x+4)<1,∴f(2ax-x2+ax2-2x+4)<f(0),
即f[(a-1)x2+2(a-1)x+4]<f(0),
∵f(x)是R上的减函数,∴(a-1)x2+2(a-1)x+4>0要恒成立.
当a=1时,不等式4>0恒成立.
当a>1时,则△=[2(a-1)]2-4(a-1)×4<0解得 1<x<5,∴1≤x<5.
点评:本题考查了抽象函数的单调性的判断方法,一般利用定义推证,强调“构造”的思路.

练习册系列答案
相关题目
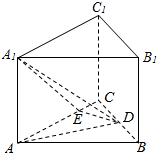 如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=
如图,在正三棱柱ABC-A1B1C1中,AB=4,AA1=| 7 |
(1)证明:平面A1DE⊥平面ACC1A1;
(2)求直线AD和平面A1DE所成角的正弦值.
设A、B、C、D是球面上的四点,AB、AC、AD两两互相垂直,且AB=5,AC=4,AD=
,则球的表面积为( )
| 23 |
| A、36π | B、64π |
| C、100π | D、144π |
f(x)=
+log4(x+1)的定义域是( )
| ||
| x-1 |
| A、(0,1)∪(1,4] |
| B、[-1,1)∪(1,4] |
| C、(-1,4) |
| D、(-1,1)∪(1,4] |