题目内容
5.已知点F(2,0),直线l:x=-2,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且$\overrightarrow{QP}•\overrightarrow{QF}=\overrightarrow{FP}•\overrightarrow{FQ}$.(1)求动点P的轨迹C的方程;
(2)点D在x轴上,且在F点的右侧,点P不在坐标原点,且|$\overrightarrow{FP}$|=|$\overrightarrow{FD}$|,直线m平行于PD,且和曲线C有且只有一个公共点E.
证明直线PE过定点,并求出定点坐标.
分析 (1)设P的坐标为(x,y),则Q(-2,y),根据向量数量积的坐标运算公式,化简等式$\overrightarrow{QP}•\overrightarrow{QF}=\overrightarrow{FP}•\overrightarrow{FQ}$,即可得到动点P的轨迹C的方程为y2=8x;
(2)求出kPD=-$\frac{{y}_{0}}{4}$,直线与抛物线的另一个交点坐标处切线的斜率,证明相等即可.
解答 (1)解:设P的坐标为(x,y),则Q(-2,y),可得$\overrightarrow{QP}$=(x+2,0),$\overrightarrow{QF}$=(4,-y),$\overrightarrow{FP}$=(x-2,y),$\overrightarrow{FQ}$=(-4,y),
∵$\overrightarrow{QP}•\overrightarrow{QF}=\overrightarrow{FP}•\overrightarrow{FQ}$,
∴(x+2)•4=(x-2)(-4)+y2,化简得y2=8x,
即动点P的轨迹C的方程为y2=8x.
(2)证明:不妨设P(x0,y0),则D(x0+4,0),∴kPD=-$\frac{{y}_{0}}{4}$,
直线PF的方程为y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),与y2=8x联立可得(x-x0)(x0x-4))=0,
∴x=x0或x=$\frac{4}{{x}_{0}}$,
即直线与抛物线的另一个交点坐标为($\frac{4}{{x}_{0}}$,-$\sqrt{\frac{32}{{x}_{0}}}$)
由y=-$\sqrt{8x}$,可得y′=-$\frac{\sqrt{2}}{\sqrt{x}}$,
∴抛物线在($\frac{4}{{x}_{0}}$,-$\sqrt{\frac{32}{{x}_{0}}}$)处切线的斜率为-$\frac{\sqrt{2{x}_{0}}}{2}$=-$\frac{{y}_{0}}{4}$,
∴E($\frac{4}{{x}_{0}}$,-$\sqrt{\frac{32}{{x}_{0}}}$),直线PE过定点F(1,0).
点评 本题着重考查了动点轨迹的求法、直线与抛物线的位置关系和向量数量积运算等知识,同时考查了逻辑思维能力、计算能力和转化化归的数学思想等知识,属于中档题.

| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
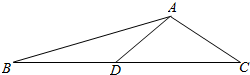 在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD
在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD