题目内容
16．已知点F为抛物线C：y2=2px（p＞0）的焦点，其到直线x=-$\frac{P}{2}$的距离为2．（1）求抛物线C的标准方程；
（2）若点P在第一象限，且横坐标为4，过点F作直线PF的垂线交直线x=-$\frac{P}{2}$于点Q，证明：直线PQ与抛物线C只有一个交点．
分析 （1）由题意，p=2，可得抛物线C的标准方程；
（2）求出直线PQ的方程与抛物线方程联立，即可证明结论．
解答 解：（1）由题意，p=2，
∴抛物线C的标准方程为y2=4x；
（2）由题意，P（4，4），F（1，0），∴kPF=$\frac{4}{3}$，
∴kQF=-$\frac{3}{4}$，
∴直线QF的方程为y=-$\frac{3}{4}$（x-1），
令x=-1，则y=$\frac{3}{2}$，
∴直线PQ的方程为y-4=$\frac{4-\frac{3}{2}}{4+1}$（x-4），即x=2y-4，
代入y2=4x，可得y2-8y+16=0，∴y=4，
∴直线PQ与抛物线C只有一个交点P．
点评 本题考查抛物线的方程，考查直线与抛物线的位置关系，正确求出直线、抛物线方程是关键．
练习册系列答案
相关题目
6．在棱长为a正方体ABCD-A1B1C1D1中，AC1和BD1相交于点O，则有（ ）
| A． | $\overrightarrow{AB}•\overrightarrow{{A_1}C}=2{a^2}$ | B． | $\overrightarrow{AB}•\overrightarrow{AC}=\sqrt{2}{a^2}$ | C． | $\overrightarrow{AB}•\overrightarrow{{A_1}O}=\frac{1}{2}{a^2}$ | D． | $\overrightarrow{BC}•\overrightarrow{AO}={a^2}$ |
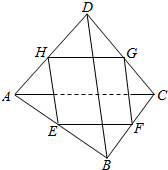如图所示，在空间四边形ABCD中，E、F、G、H分别为AB、BC、CD、AD的中点，判断平面EG与直线BD是否平行？平面EG与直线AC是否平行？直线BD与直线AC是什么位置关系？
1．若${∫}_{0}^{1}$（x2+mx）dx=$\frac{4}{3}$，则在（x2-3x+m）5的展开式中，含x项的系数为（ ）
| A． | -240 | B． | -120 | C． | 0 | D． | 120 |