题目内容
20.在平面直角坐标系x0y中,动点A的坐标为(2+$\sqrt{2}$cosα,$\sqrt{2}$sinα-1),其中α∈R.在极坐标系(以原点O为极点,以x轴非负半轴为极轴)中,直线C的方程为ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$a.(Ⅰ)判断动点A的轨迹的形状;
(Ⅱ)若直线C与动点A的轨迹有且仅有一个公共点,求实数a的值.
分析 (1)令x=2+$\sqrt{2}$cosα,y=$\sqrt{2}$sinα-1,消去参数α,得到点A的轨迹方程,判断A的轨迹;
(2)将直线C的极坐标方程化为普通方程,根据公共点个数判断出直线与圆相切,列出方程解出a.
解答 解:(1)令x=2+$\sqrt{2}$cosα,y=$\sqrt{2}$sinα-1,则cosα=$\frac{x-2}{\sqrt{2}}$,sinα=$\frac{y+1}{\sqrt{2}}$,
∴$\frac{(x-2)^{2}}{2}$+$\frac{(y+1)^{2}}{2}$=1,即(x-2)2+(y+1)2=2.
∴A的轨迹是以(2,-1)为圆心,以$\sqrt{2}$为半径的圆.
(2)∵ρcos(θ-$\frac{π}{4}$)=$\sqrt{2}$a,∴$\frac{\sqrt{2}}{2}ρcosθ$+$\frac{\sqrt{2}}{2}ρsinθ$=$\sqrt{2}a$,即ρcosθ+ρsinθ-2a=0.
∴直线C的普通方程为x+y-2a=0.
∵直线C与动点A的轨迹有且仅有一个公共点,
∴$\frac{|2-1-2a|}{\sqrt{2}}$=$\sqrt{2}$,解得a=-$\frac{1}{2}$或a=$\frac{3}{2}$.
点评 本题考查了极坐标方程,参数方程化普通方程,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
15.记max{a,b}表示a,b中较大的数,则函数f(x)=x•max{-$\frac{lnx}{ln2}$,4x2}(x>0)的递增区间为( )
| A. | (0,e) | B. | (0,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$),($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$),(e,+∞) |
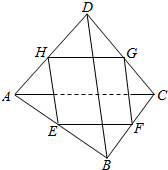 如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?
如图所示,在空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,判断平面EG与直线BD是否平行?平面EG与直线AC是否平行?直线BD与直线AC是什么位置关系?