题目内容
14.在△ABC中,已知角A,B,C的对边分别为a,b,c,bc=60$\sqrt{3}$,sinA=sinB,面积S=15$\sqrt{3}$,求a的值.分析 利用面积公式求出A,由A=B可求出C,使用正弦定理得出b,c的关系,代入bc=60$\sqrt{3}$求出b,则a=b.
解答 解:在△ABC中,∵sinA=sinB,∴A=B,a=b.
∵S=$\frac{1}{2}bc$sinA=30$\sqrt{3}$sinA=15$\sqrt{3}$,∴sinA=$\frac{1}{2}$,∴A=30°,B=30°,C=120°.
由正弦定理得$\frac{b}{sinB}=\frac{c}{sinC}$,即$\frac{b}{\frac{1}{2}}=\frac{c}{\frac{\sqrt{3}}{2}}$,∴c=$\sqrt{3}b$.
∵bc=60$\sqrt{3}$,∴b=2$\sqrt{15}$,∴a=2$\sqrt{15}$.
点评 本题考查了正余弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
19.在△ABC中,若a=9,b=10,c=12,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 最大角为120°的钝角三角形 | D. | 最大角小于120°的钝角三角形 |
11.已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示,则该正三棱锥侧视图的面积是( )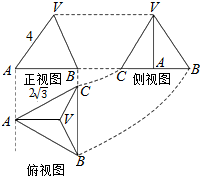

| A. | $\sqrt{39}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
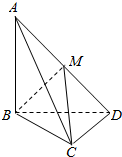 如图,三棱锥A-BCD中,AB=BD=CD=1,AD=BC=$\sqrt{2}$,AC=$\sqrt{3}$.
如图,三棱锥A-BCD中,AB=BD=CD=1,AD=BC=$\sqrt{2}$,AC=$\sqrt{3}$.