题目内容
在△ABC中,有下列结论:
①若a2>b2+c2,则△ABC为钝角三角形
②若a2=b2+c2+bc,则A为60°
③若a2+b2>c2,则△ABC为锐角三角形
④若A:B:C=1:2:3,则a:b:c=1:2:3
其中正确的个数为( )
①若a2>b2+c2,则△ABC为钝角三角形
②若a2=b2+c2+bc,则A为60°
③若a2+b2>c2,则△ABC为锐角三角形
④若A:B:C=1:2:3,则a:b:c=1:2:3
其中正确的个数为( )
| A、2 | B、3 | C、1 | D、4 |
考点:余弦定理的应用
专题:阅读型,解三角形
分析:由余弦定理.可得A为钝角,即可判断①;由余弦定理,可得cosA=
=-
,即可得到A,可判断②;
运用余弦定理可判断C为锐角,不能说明A,B也是锐角,即可判断③;运用内角和定理,求出A,B,C,再由正弦定理,即可得到三边之比,即可判断④.
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
运用余弦定理可判断C为锐角,不能说明A,B也是锐角,即可判断③;运用内角和定理,求出A,B,C,再由正弦定理,即可得到三边之比,即可判断④.
解答:
解:对于①,若a2>b2+c2,则b2+c2-a2<0,即有cosA<0,即A为钝角,故①对;
对于②,若a2=b2+c2+bc,即b2+c2-a2=-bc,则cosA=
=-
,即有A=120°,故②错;
对于③,若a2+b2>c2,则a2+b2-c2>0,即cosC>0,即C为锐角,不能说明A,B也是锐角,故③错;
对于④,若A:B:C=1:2:3,则A=30°,B=60°,C=90°,故a:b:c=sin30°:sin60°:sin90°
=1:
:2.故④错.
故选C.
对于②,若a2=b2+c2+bc,即b2+c2-a2=-bc,则cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
对于③,若a2+b2>c2,则a2+b2-c2>0,即cosC>0,即C为锐角,不能说明A,B也是锐角,故③错;
对于④,若A:B:C=1:2:3,则A=30°,B=60°,C=90°,故a:b:c=sin30°:sin60°:sin90°
=1:
| 3 |
故选C.
点评:本题考查正弦定理和余弦定理及运用,考查三角形的形状的判断,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
函数y=
cos2x的图象可以看作是把函数y=
cos(2x+
)图象( )
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
下列说法正确的是( )
| A、数列1,0,-1,-2与数列-2,-1,0,1是相同的数列 | ||||||||
| B、数列0,2,4,6,8,…,可记为{2n},n∈N+ | ||||||||
C、数列{
| ||||||||
D、数列
|
甲、乙两名运动员在某项测试中的8次成绩如下,
甲:8,9,14,15,15,16,21,22
乙:7,8,13,15,15,17,22,23
则下面说法正确的是( )
甲:8,9,14,15,15,16,21,22
乙:7,8,13,15,15,17,22,23
则下面说法正确的是( )
| A、甲的平均数和方差都比乙的大 |
| B、甲、乙的平均数相等,但甲的方差比乙的方差小 |
| C、甲、乙的平均数相等,但甲的方差比乙的方差大 |
| D、甲的平均数小于乙的平均数,但甲的方差大于乙的方差 |
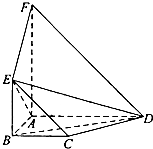 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC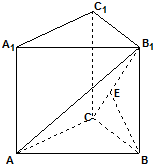 如图,在直三棱柱A1B1C1-ABC中,侧面ABB1A1是边长为2的正方形,直角三角形边满足AC=BC,E是CB1上的点,且BE⊥平面ACB1.
如图,在直三棱柱A1B1C1-ABC中,侧面ABB1A1是边长为2的正方形,直角三角形边满足AC=BC,E是CB1上的点,且BE⊥平面ACB1. 若f(x)是R上的奇函数,在[0,+∞)上图象如图所示,则满足f(x-1)>0的x的集合是
若f(x)是R上的奇函数,在[0,+∞)上图象如图所示,则满足f(x-1)>0的x的集合是