题目内容
已知数列{an}满足a1=5,anan+1=2n,则
= .
| a7 |
| a5 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:由a1=1,anan+1=2n,令n=1,求得a2的值,anan+1=2n,得anan-1=2n-1,两式相比,即得
=2,从而求得数列{an}的第5项和第7项,最终求得结果.
| an+1 |
| an-1 |
解答:
解:∵anan+1=2n,
∴anan-1=2n-1,
∴
=2,
∴数列{an}的奇数项成等比数列,偶数项成等比数列;
∴a5=5×4=20,a7=5×23=40,
故
=2
故答案为:2.
∴anan-1=2n-1,
∴
| an+1 |
| an-1 |
∴数列{an}的奇数项成等比数列,偶数项成等比数列;
∴a5=5×4=20,a7=5×23=40,
故
| a7 |
| a5 |
故答案为:2.
点评:考查由递推公式求数列中的指定项,解决方法,令n取特殊值(1,2,3,…)即可求得,体现了分类讨论的思想方法,属基础题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
f(x)=
则f[f(
)]=( )
|
| 1 |
| 4 |
| A、9 | ||
B、
| ||
| C、1 | ||
| D、3 |
将函数y=2sinxsin(
+x)的图象向右平移φ(φ>0)个单位长度,使平移后的图象仍过点(
,
),则φ的最小值为( )
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|
≥0},B={x|y=log2(x+2)},则A∩B=( )
| x-1 |
| x+1 |
| A、(-2,-1) |
| B、(-2,-1)∪[1,+∞) |
| C、[1,+∞) |
| D、(-2,-1)∪(-1,+∞) |
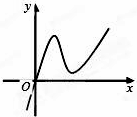 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示,若两正数a、b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示,若两正数a、b满足f(2a+b)<1,则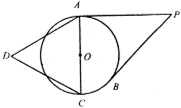 如图,半径为1的圆O外有一动点P,过P作圆O的切线PA,PB切于点A,B,以直径AC为一边作正三角形△ADC,则
如图,半径为1的圆O外有一动点P,过P作圆O的切线PA,PB切于点A,B,以直径AC为一边作正三角形△ADC,则 如图是一个平面图形的直观图,在直观图中,O′C′=O′D′=2,O′A′=3,则原平面图形的面积为
如图是一个平面图形的直观图,在直观图中,O′C′=O′D′=2,O′A′=3,则原平面图形的面积为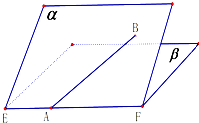 如图,二面角α-EF-β的大小是60°,线段AB?α,A在EF上,AB与β所成的角为30°,则sin∠BAF=
如图,二面角α-EF-β的大小是60°,线段AB?α,A在EF上,AB与β所成的角为30°,则sin∠BAF=