题目内容
16.设f(x)=5|x|-$\frac{1}{1+{x}^{2}}$,则使得f(2x+1)>f(x)成立的x取值范围是( )| A. | (-1,-$\frac{1}{3}$) | B. | (-3,-1) | C. | (-1,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
分析 判断函数f(x)的单调性和奇偶性,利用函数f(x)的单调性和奇偶性求解.
解答 解:函数f(x)=5|x|-$\frac{1}{1+{x}^{2}}$,
则f(-x)=5|-x|-$\frac{1}{1+({-x})^{2}}$=5|x|-$\frac{1}{1+{x}^{2}}$=f(x)为偶函数,
∵y1=5|x|是增函数,y2=-$\frac{1}{1+{x}^{2}}$也是增函数,
故函数f(x)是增函数.
那么:f(2x+1)>f(x)等价于:|2x+1|>|x|,
解得:x<-1或$x>-\frac{1}{3}$
使得f(2x+1)>f(x)成立的x取值范围是(-∞,-1)∪($-\frac{1}{3}$,+∞).
故选D.
点评 本题考查了利用函数f(x)的单调性和奇偶性求解不等式的问题.属于基础题.

练习册系列答案
相关题目
11.设全集U=Z,集合A={x|1≤x<7,x∈Z},B={x=2k-1,k∈Z},则A∩(∁UB)=( )
| A. | {1,2,3,4,5,6} | B. | {1,3,5} | C. | {2,4,6} | D. | ∅ |
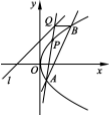 过点C(2,2)作一直线与抛物线y2=4x交于A,B两点,点P是抛物线y2=4x上到直线l:y=x+2的距离最小的点,直线AP与直线l交于点Q.
过点C(2,2)作一直线与抛物线y2=4x交于A,B两点,点P是抛物线y2=4x上到直线l:y=x+2的距离最小的点,直线AP与直线l交于点Q.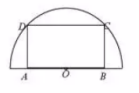 如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、
如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、