题目内容
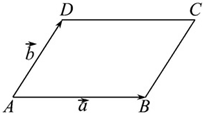如图，?ABCD中，| AB |
| a |
| AD |
| b |
（1）用
| a |
| b |
| AC |
| DB |
（2）当
| a |
| b |
| a |
| b |
| a |
| b |
（3）当
| a |
| b |
| a |
| b |
| a |
| b |
（4）
| a |
| b |
| a |
| b |
考点：向量的几何表示
专题：平面向量及应用
分析：（1）利用向量的平行四边形法则、三角形法则即可得出；
（2）当|
|=|
|时，即平行四边形ABCD为菱形时，对角线相互垂直，即可得出；
（3）当
⊥
或
•
=0时，即平行四边形ABCD为矩形时，对角线相相等，即可得出．
（4）
+
与
-
不可能为相等向量，平时四边形的对角线不共线．
（2）当|
| a |
| b |
（3）当
| a |
| b |
| a |
| b |
（4）
| a |
| b |
| a |
| b |
解答：
解：（1）∵
=
，
=
，
∴
=
+
=
+
，
=
-
=
-
．
（2）当|
|=|
|时，即平行四边形ABCD为菱形时，对角线相互垂直，即表示
+
与
-
的有向线段所在的直线互相垂直；
（3）当
⊥
或
•
=0时，即平行四边形ABCD为矩形时，对角线相相等，即|
+
|=|
-
|．
（4）
+
与
-
不可能为相等向量，因为它们不共线．
| AB |
| a |
| AD |
| b |
∴
| AC |
| AB |
| AD |
| a |
| b |
| DB |
| AB |
| AD |
| a |
| b |
（2）当|
| a |
| b |
| a |
| b |
| a |
| b |
（3）当
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（4）
| a |
| b |
| a |
| b |
点评：本题考查了向量的平行四边形法则、三角形法则、平行四边形菱形矩形的性质、共线向量，考查了数形结合的思想方法，考查了推理能力，属于基础题．
练习册系列答案
相关题目
已知椭圆和双曲线右公共焦点F1、F2，P是它们的一个公共点，且∠F1PF2=
，若双曲线的离心率为
，则椭圆的离心率为（ ）
| π |
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
给出下列命题：其中正确的命题个数是（ ）
（1）垂直于同一直线的两直线平行．
（2）平行于同一平面的两直线平行．
（3）平行于同一直线的两直线平行．
（4）平面内不相交的两直线平行．
（1）垂直于同一直线的两直线平行．
（2）平行于同一平面的两直线平行．
（3）平行于同一直线的两直线平行．
（4）平面内不相交的两直线平行．
| A、4 | B、3 | C、2 | D、1 |
不等式2x3-7x2-4x＜0的解为（ ）
A、x＜-
| ||
B、-
| ||
C、-
| ||
| D、无解 |
4张奖券中只有1张能中奖，现分别由4名同学无放回地抽取．若已知第一名同学没有抽到中奖券，则第二名同学抽到中奖券的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、1 |