题目内容
已知双曲线的方程为
-x2=1，点A的坐标为（0，-
），B是圆（x-
）2+y2=1上的点，点M在双曲线的上支上，则|MA|+|MB|的最小值为 ．
| y2 |
| 4 |
| 5 |
| 5 |
考点：双曲线的简单性质
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：设点D的坐标为（0，
），则点A，D是双曲线的焦点，利用双曲线的定义，可得|MA|-|MD|=2a=4．于是|MA|+|MB|=4+|MB|+|MD|≥4+|BD|，再利用|BD|≥|CD|-r即可．
| 5 |
解答：
解：设点D的坐标为（0，
），则点A，D是双曲线的焦点，
由双曲线的定义，得|MA|-|MD|=2a=4．
∴|MA|+|MB|=4+|MB|+|MD|≥4+|BD|，
又B是圆（x-
）2+y2=1上的点，
则圆的圆心为C（
，0），半径为1，
故|BD|≥|CD|-1=
-1=
-1，
从而|MA|+|MB|≥4+|BD|≥
+3，
当点M，B在线段CD上时取等号，即|MA|+|MB|的最小值为
+3．
故答案为：
+3．
| 5 |
由双曲线的定义，得|MA|-|MD|=2a=4．
∴|MA|+|MB|=4+|MB|+|MD|≥4+|BD|，
又B是圆（x-
| 5 |
则圆的圆心为C（
| 5 |
故|BD|≥|CD|-1=
| 5+5 |
| 10 |
从而|MA|+|MB|≥4+|BD|≥
| 10 |
当点M，B在线段CD上时取等号，即|MA|+|MB|的最小值为
| 10 |
故答案为：
| 10 |
点评：熟练掌握双曲线的定义和性质及其圆外一点到圆上一点距离的最小值是解题的关键．
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0）的左右焦点分别为F1，F2，若双曲线右支上存在一点P，使得F2关于直线PF1的对称点恰在y轴上，则该双曲线的离心率e的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、1＜e＜
| ||||
B、e＞
| ||||
C、e＞
| ||||
D、1＜e＜
|
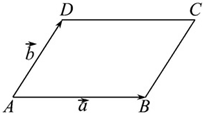如图，?ABCD中，