题目内容
在平面直角坐标系中,定义:一条直线经过一个点(x,y),若x,y都是整数,就称该直线为完美直线,这个点叫直线的完美点,若一条直线上没有完美点,则就称它为遗憾直线.现有如下几个命题:
①如果k与b都是无理数,则直线y=kx+b一定是遗憾直线;
②“直线y=kx+b是完美直线”的充要条件是“k与b都是有理数”;
③存在恰有一个完美点的完美直线;
④完美直线l经过无穷多个完美点,当且仅当直线l经过两个不同的完美点.
其中正确的命题是 .(写出所有正确命题的编号)
①如果k与b都是无理数,则直线y=kx+b一定是遗憾直线;
②“直线y=kx+b是完美直线”的充要条件是“k与b都是有理数”;
③存在恰有一个完美点的完美直线;
④完美直线l经过无穷多个完美点,当且仅当直线l经过两个不同的完美点.
其中正确的命题是
考点:命题的真假判断与应用
专题:直线与圆,简易逻辑
分析:①不正确,如果取k=
,b=
,那么直线y=
x+
经过完美点(-1,0),是完美直线;
②由①知当k=b=
时,k与b均为无理数,但是直线y=
x+
是完美直线,即可判断出正误;
③设直线方程为y=
x,只经过了一个完美点(0,0),即可判断出正误;
④,设y=kx为过原点的完美直线,若此直线l过不同的完美点(x1,y1)和(x2,y2),可得(x1-x2,y1-y2)也在完美直线y=kx上,且(x1-x2,y1-y2)也为完美点,通过这种方法得到直线l经过无穷多个完美点.
| 3 |
| 3 |
| 3 |
| 3 |
②由①知当k=b=
| 3 |
| 3 |
| 3 |
③设直线方程为y=
| 5 |
④,设y=kx为过原点的完美直线,若此直线l过不同的完美点(x1,y1)和(x2,y2),可得(x1-x2,y1-y2)也在完美直线y=kx上,且(x1-x2,y1-y2)也为完美点,通过这种方法得到直线l经过无穷多个完美点.
解答:
解:对于①,如果取k=
,b=
,那么直线y=
x+
经过完美点(-1,0),是完美直线,所以①错误;
对于②,由①知当k=b=
时,k与b均为无理数,但是直线y=
x+
是完美直线,所以②错误;
对于③,设直线方程为y=
x,只经过了一个完美点(0,0),所以③正确;
对于④,设y=kx为过原点的完美直线,若此直线l过不同的完美点(x1,y1)和(x2,y2),把两点代入完美直线l的方程得y1=kx1,y2=kx2,两式相减得y1-y2=k(x1-x2),则(x1-x2,y1-y2)也在完美直线y=kx上,且(x1-x2,y1-y2)也为完美点,通过这种方法得到直线l经过无穷多个完美点,所以④正确.
故答案为:③④.
| 3 |
| 3 |
| 3 |
| 3 |
对于②,由①知当k=b=
| 3 |
| 3 |
| 3 |
对于③,设直线方程为y=
| 5 |
对于④,设y=kx为过原点的完美直线,若此直线l过不同的完美点(x1,y1)和(x2,y2),把两点代入完美直线l的方程得y1=kx1,y2=kx2,两式相减得y1-y2=k(x1-x2),则(x1-x2,y1-y2)也在完美直线y=kx上,且(x1-x2,y1-y2)也为完美点,通过这种方法得到直线l经过无穷多个完美点,所以④正确.
故答案为:③④.
点评:本题考查了新定义“完美直线”、通过举反例否定一个命题的方法,考查了推理能力,属于中档题.

练习册系列答案
相关题目
函数f(x)图象的一部分如图所示,则f(x)的解析式可为( )


A、f(x)=4sin
| ||
B、f(x)=3.5sin
| ||
C、f(x)=3.5sin
| ||
D、f(x)=4sin
|
设数列1,1+2,1+2+3,…的前n项的和为Sn,则Sn等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
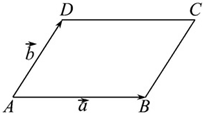 如图,?ABCD中,
如图,?ABCD中,