题目内容
4张奖券中只有1张能中奖,现分别由4名同学无放回地抽取.若已知第一名同学没有抽到中奖券,则第二名同学抽到中奖券的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点:等可能事件的概率,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:本题是一个计算概率的问题,由题意知已经知道第一名同学没有抽到中奖奖券,问题转化为研究三张奖券3个人抽取中奖的情况,根据无放回抽取的概率意义,可得到中奖的概率.
解答:
解:由题意,由于第一名同学没有抽到中奖奖券,问题转化为研究两张奖券三个人抽取中奖的情况,
由于无放回的抽样是一个等可能抽样,故此3个同学抽到中奖奖券的概率是一样的都是
故选:B.
由于无放回的抽样是一个等可能抽样,故此3个同学抽到中奖奖券的概率是一样的都是
| 1 |
| 3 |
故选:B.
点评:本题考查等可能事件的概率,理解无放回抽样是一个等可能抽样是求解本题的关键,等可能抽样,第几次抽取中奖的是相等的,都等于
.
| 有奖奖券数 |
| 奖券总数 |

练习册系列答案
相关题目
若函数f(x)=3-|x-2|-c的图象与x轴有交点,则实数c的取值范围是( )
| A、[-1,0) |
| B、[0,1] |
| C、(0,1] |
| D、[1,+∞) |
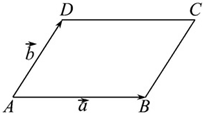 如图,?ABCD中,
如图,?ABCD中,