题目内容
公比为q的等比数列{an}的前n项和为Sn,且a2+a4=20,a3+a5=40,设Tn=n(Sn+q),则数列{Tn}的前n项和为________.
(n-1)·2n+2+4
[解析] 依题意,得q= =2,a1q+a1q3=10a1=20,a1=2,Sn+q=
=2,a1q+a1q3=10a1=20,a1=2,Sn+q=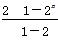 +2=2n+1,Tn=n·2n+1.记数列{Tn}的前n项和为Bn,则
+2=2n+1,Tn=n·2n+1.记数列{Tn}的前n项和为Bn,则
Bn=1·22+2·23+3·24+…+n·2n+1,①
2Bn=1·23+2·24+…+(n-1)·2n+1+n·2n+2,②
由②-①,得Bn=-22-23-24-…-2n+1+n·2n+2=-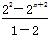 +n·2n+2=(n-1)·2n+2+4,因此数列{Tn}的前n项和为(n-1)·2n+2+4.
+n·2n+2=(n-1)·2n+2+4,因此数列{Tn}的前n项和为(n-1)·2n+2+4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图像过点
的图像过点 ,其反函数的图像过点
,其反函数的图像过点 ,则
,则 = __________
= __________ ,b=2acos B,c=1,则△ABC的面积等于( )
,b=2acos B,c=1,则△ABC的面积等于( )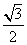 B.
B.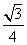 C.
C.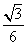 D.
D.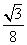
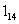 01)2转换成十进制数是( )
01)2转换成十进制数是( )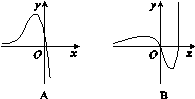
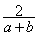 的最小值是
的最小值是