题目内容
如图所示,某电力公司为保护一墙角处的电塔,计划利用墙OA,OB,再修建一长度为AB的围栏,围栏的造价与AB的长度成正比.现已知墙角∠AOB的度数为120°,当△AOB的面积为 时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )
时,就可起到保护作用.则当围栏的造价最低时,∠ABO=( )
A.30° B.45°
C.60° D.90°
A
[解析] 只要AB的长度最小,围栏的造价就最低.设OA=a,OB=b,则由余弦定理,得AB2=a2+b2-2abcos 120°=a2+b2+ab≥2ab+ab=3ab(当且仅当a=b时取等号),又S△AOB=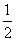 absin 120°=
absin 120°= ,所以ab=4.故AB2≥12,即AB的最小值为2
,所以ab=4.故AB2≥12,即AB的最小值为2 .由a=b及3ab=12,得a=b=2.由正弦定理,得sin ∠ABO=
.由a=b及3ab=12,得a=b=2.由正弦定理,得sin ∠ABO=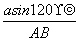 =
= ×
×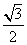 =
=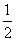 .故∠ABO=30°,故选A.
.故∠ABO=30°,故选A.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 ,
,
 ,若
,若
 ,则
,则 且
且 ”的逆否命题是__
”的逆否命题是__ ,则___
,则___ 的图象如图所示,则f(x)的解析式为( )
的图象如图所示,则f(x)的解析式为( )

 +2sin x.
+2sin x. ,求f(A)的值;
,求f(A)的值; ,b=2acos B,c=1,则△ABC的面积等于( )
,b=2acos B,c=1,则△ABC的面积等于( )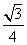 C.
C.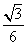 D.
D.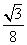
 D.-
D.-