题目内容
已知椭圆C：
+
=1（a＞b＞0）的离心率为
，过右焦点F且斜率为k（k＞0）的直线与C相交与A，B两点，若
=2
，则k=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| AF |
| FB |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：首先，作椭圆的右准线，然后，利用椭圆的第二定义，将距离转化，最后，结合直角三角形中的边角关系求解斜率．
解答：
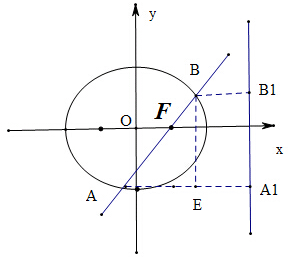解：设l为椭圆的右准线，过A、B作AA1，BB1垂直于l，A1，B1为垂足，
过B作BE⊥AA1于E，根据椭圆的第二定义，得
|AA1|=
，|BB1|=
，
∵
=2
，∴cos∠BAE=
=
=
=
，
∴tan∠BAE=
．
∴k=
．
故选：B．
解：设l为椭圆的右准线，过A、B作AA1，BB1垂直于l，A1，B1为垂足，过B作BE⊥AA1于E，根据椭圆的第二定义，得
|AA1|=
| |AF| |
| e |
| |BF| |
| e |
∵
| AF |
| FB |
| |AE| |
| |AB| |
| ||
| 3|BF| |
| 1 |
| 3e |
2
| ||
| 9 |
∴tan∠BAE=
| ||
| 2 |
∴k=
| ||
| 2 |
故选：B．
点评：本题重点考查了椭圆的第二定义、椭圆的几何性质等，属于中档题．解题关键是准确利用椭圆的定义，将问题等价转化．
练习册系列答案
名校课堂系列答案
相关题目
如图有一个几何体的三视图（单位：cm），试画出它的直观图，并计算这个几何体的体积．
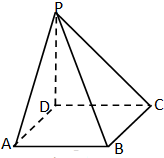四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥底面ABCD，PA=2AB，则四棱锥P-ABCD外接球的表面积为（ ）| A、24π | B、8π |
| C、6π | D、36π |
