题目内容
若m>0,点P(m,
)在双曲线
-
=1上,则点P到该双曲线左焦点的距离为 .
| 5 |
| 2 |
| x2 |
| 4 |
| y2 |
| 5 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:把点P(m,
)代入双曲线
-
=1可得m,再利用两点之间的距离公式即可得出.
| 5 |
| 2 |
| x2 |
| 4 |
| y2 |
| 5 |
解答:
解:∵m>0,点P(m,
)在双曲线
-
=1上,
∴
-
=1,解得m=3.
∴P(3,
).
双曲线的左焦点F(-3,0),
∴点P到该双曲线左焦点的距离=
=
.
故答案为:
.
| 5 |
| 2 |
| x2 |
| 4 |
| y2 |
| 5 |
∴
| m2 |
| 4 |
| 25 |
| 4×5 |
∴P(3,
| 5 |
| 2 |
双曲线的左焦点F(-3,0),
∴点P到该双曲线左焦点的距离=
62+(
|
| 13 |
| 2 |
故答案为:
| 13 |
| 2 |
点评:本题考查了点与双曲线的关系、两点之间的距离公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(sinx)=cos3x,则f(cos10°)的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
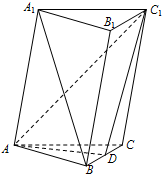 如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.
如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.