题目内容
3.已知f(x)=$\left\{\begin{array}{l}{{e}^{x}+ax,x>0}\\{0,x=0}\\{{e}^{-x}-ax,x<0}\end{array}\right.$,若函数f(x)有三个零点,则实数a的值是( )| A. | e | B. | $\frac{1}{e}$ | C. | -$\frac{1}{e}$ | D. | -e |
分析 判断f(x)的奇偶性,根据f(x)的零点个数可知ex+ax=0在(0,+∞)上只有一解,即直线y=-ax与y=ex相切,根据导数的几何意义列方程组解出a即可.
解答 解:若x>0,则f(-x)=ex+ax=f(x),
同理,当x<0时,f(-x)=f(x),
∴f(x)是偶函数,
又f(0)=0,∴x=0是f(x)的一个零点,
∵f(x)有三个零点,
∴f(x)在(0,+∞)上只有一个零点.
当x>0时,令f(x)=0得ex=-ax,
∴直线y=-ax与y=ex相切.
设切点坐标为(x0,y0),则$\left\{\begin{array}{l}{{e}^{{x}_{0}}=-a}\\{-a{x}_{0}={e}^{{x}_{0}}}\end{array}\right.$,
解得x0=1,a=-e.
故选:D.
点评 本题考查了函数奇偶性的判断与性质,函数零点的个数判定,导数的几何意义,属于中档题.

练习册系列答案
相关题目
14.一个几何体的三视图如图所示,则这个几何体的表面积是( )
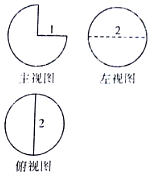

| A. | 3π | B. | 4π | C. | 5π | D. | $\frac{7π}{3}$ |
11. 若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以CD为直径的半圆内的概率是( )
若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以CD为直径的半圆内的概率是( )
 若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以CD为直径的半圆内的概率是( )
若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以CD为直径的半圆内的概率是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
18.设$\overrightarrow{a}$,$\overrightarrow{b}$为向量,则“$\overrightarrow{a}$•$\overrightarrow{b}$=0”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.若不等式|x-2|+|x-3|<3的解集是(a,b),则$\int_a^b{(\sqrt{x}-1)dx=}$( )
| A. | $\frac{7}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{5}{3}$ | D. | 3 |
15.cos2165°-sin215°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
13.设复数z1,z2在复平面内的对应点关于原点对称,z1=2-i,则z1•z2=( )
| A. | -5 | B. | -3+4i | C. | -3 | D. | -5+4i |