题目内容
14.一个几何体的三视图如图所示,则这个几何体的表面积是( )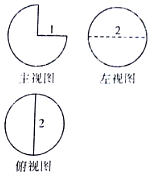
| A. | 3π | B. | 4π | C. | 5π | D. | $\frac{7π}{3}$ |
分析 根据三视图知,该几何体为半径为1的球体,挖去$\frac{1}{4}$球体,
结合图中数据求出它的表面积.
解答 解:根据三视图知,
该几何体为半径为1的球体,挖去$\frac{1}{4}$球体,
该几何体的表面积为
S=$\frac{3}{4}$×4πR2+2×$\frac{1}{2}$πR2=4πR2=4π.
故选:B.
点评 本题考查了三视图的应用问题,解题的关键由三视图想象出直观图,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | 2 |
19.已知定义在R上的函数f(x)的导函数为f′(x),对任意x∈R满足f(x)+f′(x)<0,则下列结论正确的是( )
| A. | 2f(ln2)>3f(ln3) | B. | 2f(ln2)<3f(ln3) | C. | 2f(ln2)≥3f(ln3) | D. | 2f(ln2)≤3f(ln3) |
3.已知f(x)=$\left\{\begin{array}{l}{{e}^{x}+ax,x>0}\\{0,x=0}\\{{e}^{-x}-ax,x<0}\end{array}\right.$,若函数f(x)有三个零点,则实数a的值是( )
| A. | e | B. | $\frac{1}{e}$ | C. | -$\frac{1}{e}$ | D. | -e |
4.函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )
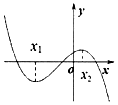

| A. | a>0,b>0,c>0,d<0 | B. | a>0,b>0,c<0,d<0 | C. | a<0,b<0,c>0,d>0 | D. | a>0,b>0,c>0,d>0 |
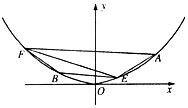 如图,已知线段AE,BF为抛物线C:x2=2py(p>0)的两条弦,点E、F不重合.函数y=ax(a>0且a≠1)的图象所恒过的定点为抛物线C的焦点.
如图,已知线段AE,BF为抛物线C:x2=2py(p>0)的两条弦,点E、F不重合.函数y=ax(a>0且a≠1)的图象所恒过的定点为抛物线C的焦点.