题目内容

13．设复数z1，z2在复平面内的对应点关于原点对称，z1=2-i，则z1•z2=（　　）
A．-5B．-3+4iC．-3D．-5+4i

分析 复数z1，z2在复平面内的对应点关于原点对称，z1=2-i，可得z2=-2+i．再利用复数的运算法则即可得出．

解答 解：∵复数z1，z2在复平面内的对应点关于原点对称，z1=2-i，∴z2=-2+i．
则z1•z2=（2-i）（-2+i）=-3+4i．
故选：B．

点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
3．已知f（x）=$\left\{\begin{array}{l}{{e}^{x}+ax，x＞0}\\{0，x=0}\\{{e}^{-x}-ax，x＜0}\end{array}\right.$，若函数f（x）有三个零点，则实数a的值是（　　）
A．eB．$\frac{1}{e}$C．-$\frac{1}{e}$D．-e
4．函数f（x）=ax3+bx2+cx+d的图象如图所示，则下列结论成立的是（　　）
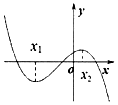
A．a＞0，b＞0，c＞0，d＜0B．a＞0，b＞0，c＜0，d＜0C．a＜0，b＜0，c＞0，d＞0D．a＞0，b＞0，c＞0，d＞0
1．已知函数f（x）=|x•ex|，g（x）=f2（x）+λf（x），若方程g（x）=-1有且仅有4个不同的实数解，则实数λ的取值范围是（-∞，-e-$\frac{1}{e}$）．
8．如图是总体密度曲线，下列说法正确的是（　　）
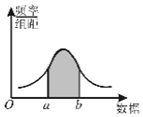
A．组距越大，频率分布折线图越接近于它
B．样本容量越小，频率分布折线图越接近于它
C．阴影部分的面积代表总体在（a，b）内取值的百分比
D．阴影部分的平均高度代表总体在（a，b）内取值的百分比
18．设α∈（0，$\frac{π}{2}$），β∈（0，$\frac{π}{2}$），且$\frac{sinα}{cosα}$=$\frac{cosβ}{1-sinβ}$，则（　　）
A．2α+β=$\frac{π}{2}$B．2α-β=$\frac{π}{2}$C．α+2β=$\frac{π}{2}$D．α-2β=$\frac{π}{2}$
5．设数列{an}满足a1=a，an+1=$\frac{a_n^2-2}{{{a_n}+1}}$（n∈N），若数列{an}是常数列，则a=（　　）
A．-2B．-1C．0D．（-1）n
2．已知角α的顶点在坐标原点，始边与x轴的非负半轴重合，终边经过点（-$\sqrt{3}$，2），则tan（α-$\frac{π}{6}$）的值为（　　）
A．-3$\sqrt{3}$B．-$\frac{\sqrt{3}}{5}$C．-$\frac{5\sqrt{3}}{3}$D．-$\frac{3\sqrt{3}}{5}$
3．某企业生产的某种产品被检测出其中一项质量指标存在问题．该企业为了检查生产该产品的甲，乙两条流水线的生产情况，随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本，测出它们的这一项质量指标值．若该项质量指标值落在（195，210]内，则为合格品，否则为不合格品．表1是甲流水线样本的频数分布表，如图是乙流水线样本的频率分布直方图．
甲流水线样本的频数分布表
质量指标值频数
（190，195]9
（195，200]10
（200，205]17
（205，210]8
（210，215]6
（Ⅰ）根据图1，估计乙流水线生产产品该质量指标值的中位数；
（Ⅱ）若将频率视为概率，某个月内甲，乙两条流水线均生产了5000件产品，则甲，乙两
条流水线分别生产出不合格品约多少件？
（Ⅲ）根据已知条件完成下面2×2列联表，并回答是否有85%的把握认为“该企业生产的这
种产品的质量指标值与甲，乙两条流水线的选择有关”？
甲生产线乙生产线合计
合格品
不合格品
合计
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d为样本容量）
P（K2≥k）0.150.100.050.0250.0100.0050.001
k2.0722.7063.8415.0246.6357.87910.828

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网