题目内容
12.已知x,y均为正实数,若$\overrightarrow{a}$=(x,y-1),$\overrightarrow{b}$=(2,1),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\frac{1}{x}+\frac{2}{y}$的最小值是8.分析 $\overrightarrow{a}$⊥$\overrightarrow{b}$,考点$\overrightarrow{a}$•$\overrightarrow{b}$=0,即2x+y=1.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴$\overrightarrow{a}$•$\overrightarrow{b}$=2x+y-1=0,即2x+y=1.
又x,y均为正实数,
则$\frac{1}{x}+\frac{2}{y}$=(2x+y)$(\frac{1}{x}+\frac{2}{y})$=4+$\frac{y}{x}+\frac{4x}{y}$≥4+2$\sqrt{\frac{y}{x}•\frac{4x}{y}}$=8,当且仅当y=2x=$\frac{1}{2}$时取等号.
故答案为:8.
点评 本题考查了“乘1法”与基本不等式的性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
3.已知f(x)=$\left\{\begin{array}{l}{{e}^{x}+ax,x>0}\\{0,x=0}\\{{e}^{-x}-ax,x<0}\end{array}\right.$,若函数f(x)有三个零点,则实数a的值是( )
| A. | e | B. | $\frac{1}{e}$ | C. | -$\frac{1}{e}$ | D. | -e |
7.用0,1,2,…,299给300名高三学生编号,并用系统抽样的方法从中抽取15名学生的数学成绩进行质量分析,若第一组抽取的学生的编号为8,则第三组抽取的学生编号为( )
| A. | 20 | B. | 28 | C. | 40 | D. | 48 |
4.函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )
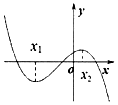

| A. | a>0,b>0,c>0,d<0 | B. | a>0,b>0,c<0,d<0 | C. | a<0,b<0,c>0,d>0 | D. | a>0,b>0,c>0,d>0 |
2.已知角α的顶点在坐标原点,始边与x轴的非负半轴重合,终边经过点(-$\sqrt{3}$,2),则tan(α-$\frac{π}{6}$)的值为( )
| A. | -3$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{5}$ | C. | -$\frac{5\sqrt{3}}{3}$ | D. | -$\frac{3\sqrt{3}}{5}$ |
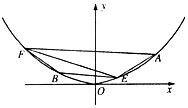 如图,已知线段AE,BF为抛物线C:x2=2py(p>0)的两条弦,点E、F不重合.函数y=ax(a>0且a≠1)的图象所恒过的定点为抛物线C的焦点.
如图,已知线段AE,BF为抛物线C:x2=2py(p>0)的两条弦,点E、F不重合.函数y=ax(a>0且a≠1)的图象所恒过的定点为抛物线C的焦点.