题目内容
15.cos2165°-sin215°=( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 由诱导公式,二倍角的余弦公式可得 cos215°-sin215°=cos30°,从而得到结果.
解答 解:由诱导公式,二倍角的余弦公式可得,
cos2165°-sin215°=cos215°-sin215°=cos30°=$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题主要考查诱导公式,二倍角的余弦公式的应用,考查特殊角的三角函数值,属于基础题.

练习册系列答案
相关题目
3.已知f(x)=$\left\{\begin{array}{l}{{e}^{x}+ax,x>0}\\{0,x=0}\\{{e}^{-x}-ax,x<0}\end{array}\right.$,若函数f(x)有三个零点,则实数a的值是( )
| A. | e | B. | $\frac{1}{e}$ | C. | -$\frac{1}{e}$ | D. | -e |
7.用0,1,2,…,299给300名高三学生编号,并用系统抽样的方法从中抽取15名学生的数学成绩进行质量分析,若第一组抽取的学生的编号为8,则第三组抽取的学生编号为( )
| A. | 20 | B. | 28 | C. | 40 | D. | 48 |
4.函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论成立的是( )
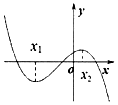

| A. | a>0,b>0,c>0,d<0 | B. | a>0,b>0,c<0,d<0 | C. | a<0,b<0,c>0,d>0 | D. | a>0,b>0,c>0,d>0 |
5.设数列{an}满足a1=a,an+1=$\frac{a_n^2-2}{{{a_n}+1}}$(n∈N),若数列{an}是常数列,则a=( )
| A. | -2 | B. | -1 | C. | 0 | D. | (-1)n |