题目内容
过点A（1，-3）的圆x2+y2=10的切线的方程是 ．
考点：直线与圆的位置关系
专题：直线与圆
分析：判断点A在圆上，即A是切点，即可求出切线方程．
解答：
解：∵点A（1，-3）满足圆x2+y2=10，
∴点A是切点，
则OA的斜率k=-3，
则切线的斜率k=
，
故所求的切线方程为y+3=
（x-1），即x-3y-10=0，
故答案为：
∴点A是切点，
则OA的斜率k=-3，
则切线的斜率k=
| 1 |
| 3 |
故所求的切线方程为y+3=
| 1 |
| 3 |
故答案为：
点评：本题主要考查圆的切线的求解，根据条件确定A是切点是解决本题的关键．
练习册系列答案
字词句段篇系列答案
相关题目
命题“对任意 x∈R，都有 x2≥0”的否定为（ ）
| A、对任意 x∈R，都有 x2＜0 |
| B、不存在 x∈R，使得 x2＜0 |
| C、存在 x0∈R，使得 x02≥0 |
| D、存在 x0∈R，使得 x02＜0 |
已知椭圆C：
+x2=1，直线l：9x+y-5=0与椭圆C相交于A、B两点，点P为弦AB的中点，则点P的坐标为（ ）
| y2 |
| 9 |
A、（
| ||||
B、（-
| ||||
| C、（1，-4） | ||||
| D、（-1，14） |
球O的一个截面圆的圆心为M，圆M的半径为
，OM的长度为球O的半径的一半，则球O的表面积为（ ）
| 3 |
| A、4π | ||
B、
| ||
| C、12π | ||
| D、16π |
图中的程序框图所描述的算法称为欧几里得辗转相除法． 若输入m=209，n=121，则输出m=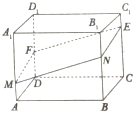
如图4所示，已知直四棱柱ABCD-A1B1C1D1的底面是棱形，其边长为4，∠BAD=60°，点M，N，E分别在棱AA1，BB1，CC1上，过M，N，E的面与棱DD1交于F，AM=2，BN=4，CE=5．求：