题目内容
已知下列直线的倾斜角,求直线的斜率:
(1)a=30°
(2)a=45°
(3)a=120°
(4)a=135°.
(1)a=30°
(2)a=45°
(3)a=120°
(4)a=135°.
考点:直线的斜率
专题:直线与圆
分析:根据直线斜率的定义,当a≠90°,斜率k=tanα,计算即可.
解答:
解:根据直线斜率的定义,得;
(1)当a=30°时,斜率k=tan30°=
;
(2)当a=45°时,斜率k=tan45°=1;
(3)当a=120°时,斜率k=tan120°=tan(180°-60°)=-tan60°=-
;
(4)当a=135°时,斜率k=tan135°=tan(180°-45°)=-tan45°=-1.
(1)当a=30°时,斜率k=tan30°=
| ||
| 3 |
(2)当a=45°时,斜率k=tan45°=1;
(3)当a=120°时,斜率k=tan120°=tan(180°-60°)=-tan60°=-
| 3 |
(4)当a=135°时,斜率k=tan135°=tan(180°-45°)=-tan45°=-1.
点评:本题考查了根据直线的倾斜角求直线的斜率的应用问题,是基础题目.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
存在实数a使得方程cosx=a在[0,2π]上有两个不相等的实数根x1,x2,则sin
=( )
| x1+x2 |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
执行如图所示的程序框图,若p=0.7,则输出的n为( )


| A、2 | B、3 | C、4 | D、5 |
为了得到函数y=sin2x(x∈R)的图象,可以把函数y=sin(3x+
)(x∈R)的图象上所有点的( )
| π |
| 6 |
A、纵坐标不变,横坐标伸长到原来的
| ||||
B、纵坐标不变,横坐标伸长到原来的
| ||||
C、纵坐标不变,横坐标缩短到原来的
| ||||
D、纵坐标不变,横坐标缩短到到原来的
|
函数f(x)=x-2+lnx的零点所在的一个区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
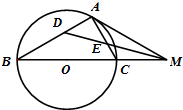 已知Rt△ABC(∠A=90°)的外接圆为圆O,过A的切线AM交BC于点M,过M作直线交AB,AC于点D,E,且AD=AE
已知Rt△ABC(∠A=90°)的外接圆为圆O,过A的切线AM交BC于点M,过M作直线交AB,AC于点D,E,且AD=AE