题目内容
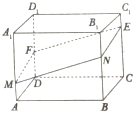 如图4所示,已知直四棱柱ABCD-A1B1C1D1的底面是棱形,其边长为4,∠BAD=60°,点M,N,E分别在棱AA1,BB1,CC1上,过M,N,E的面与棱DD1交于F,AM=2,BN=4,CE=5.求:
如图4所示,已知直四棱柱ABCD-A1B1C1D1的底面是棱形,其边长为4,∠BAD=60°,点M,N,E分别在棱AA1,BB1,CC1上,过M,N,E的面与棱DD1交于F,AM=2,BN=4,CE=5.求:(1)求证:平面MNEF⊥平面ABB1A1;
(2)求平面MNEF与底面ABCD所成的锐二面角的余弦值.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知MF∥NE,MN∥EF,从而四边形MNEF是平行四边形,取MN中点G,AB中点Q,QG是梯形的中位线,从而QG=
(AM+BN)=3,进而四边形QGFD为平行四边形,由△ABD是正三角形,得DQ⊥平面AA1B1B,由此能平面MNEF⊥平面AA1B1B.
(2)以DQ、DC、DD1为坐标轴建立如图所示的空间直角坐标系,分别求出平面MNEF的法向量和平面ABCD的法向量,由此利用向量法能求出平面MNEF与底面ABCD所成的锐二面角的余弦值.
| 1 |
| 2 |
(2)以DQ、DC、DD1为坐标轴建立如图所示的空间直角坐标系,分别求出平面MNEF的法向量和平面ABCD的法向量,由此利用向量法能求出平面MNEF与底面ABCD所成的锐二面角的余弦值.
解答:
(1)证明:∵平面ADD1A1∩平面EFMN=MF,平面BB1C1C∩平面EFMN=NE,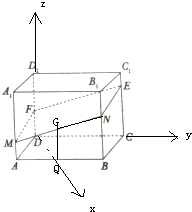
∴MF∥NE,同理MN∥EF,∴四边形MNEF是平行四边形,
∵梯形ACEM与梯形BNFD有公共中位线,
∴AM+CE=BN+DF,∴DF=3,
取MN中点G,AB中点Q,∵QG是梯形ABNM的中位线,∴QG=
(AM+BN)=3,
∴QG∥DF,QG=DF,∴四边形QGFD为平行四边形,∴FG∥DG,
又△ABD是正三角形,且Q为AB的中点,
∴DQ⊥AB,又DQ⊥AA1,∴DQ⊥平面AA1B1B,
∴FG⊥平面AA1B1B,又FG?平面MNEF,∴平面MNEF⊥平面AA1B1B.
(2)解:以DQ、DC、DD1为坐标轴建立如图所示的空间直角坐标系,
F(0,0,3),G(2
,0,3),M(2
,-2,2),
=(2
,-2,-1_,
=(2
,0,0),
设平面MNEF的法向量
=(x,y,z),
则
,取y=-1,得
=(0,-1,2),
又平面ABCD的法向量
=(0,0,1),
cos<
,
>=
=
=
,
∴平面MNEF与底面ABCD所成的锐二面角的余弦值为
.

∴MF∥NE,同理MN∥EF,∴四边形MNEF是平行四边形,
∵梯形ACEM与梯形BNFD有公共中位线,
∴AM+CE=BN+DF,∴DF=3,
取MN中点G,AB中点Q,∵QG是梯形ABNM的中位线,∴QG=
| 1 |
| 2 |
∴QG∥DF,QG=DF,∴四边形QGFD为平行四边形,∴FG∥DG,
又△ABD是正三角形,且Q为AB的中点,
∴DQ⊥AB,又DQ⊥AA1,∴DQ⊥平面AA1B1B,
∴FG⊥平面AA1B1B,又FG?平面MNEF,∴平面MNEF⊥平面AA1B1B.
(2)解:以DQ、DC、DD1为坐标轴建立如图所示的空间直角坐标系,
F(0,0,3),G(2
| 3 |
| 3 |
| FM |
| 3 |
| FG |
| 3 |
设平面MNEF的法向量
| n |
则
|
| n |
又平面ABCD的法向量
| m |
cos<
| n |
| m |
| ||||
|
|
| 2 | ||
|
2
| ||
| 5 |
∴平面MNEF与底面ABCD所成的锐二面角的余弦值为
2
| ||
| 5 |
点评:本题考查线面关系、直线与平面所成的角、二面角、梯形及平行四边形等基础知识,考查思维能力、空间想象能力,考查应用向量知识解决数学问题的能力.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知数列{an}中,有an+1=an+4,且a1+a4=14.
(1)求{an}的通项公式an与前n项和公式Sn;
(2)令bn=
,若{bn}是等差数列,求数列{
}的前n项和Tn.
(1)求{an}的通项公式an与前n项和公式Sn;
(2)令bn=
| Sn |
| n+k |
| 1 |
| bnbn+1 |
将函数y=sin(2x+
)的图象沿x轴向左平移m(m>0)个单位后,得到一个奇函数的图象,则m的最小值为( )
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
为了得到函数y=sin2x(x∈R)的图象,可以把函数y=sin(3x+
)(x∈R)的图象上所有点的( )
| π |
| 6 |
A、纵坐标不变,横坐标伸长到原来的
| ||||
B、纵坐标不变,横坐标伸长到原来的
| ||||
C、纵坐标不变,横坐标缩短到原来的
| ||||
D、纵坐标不变,横坐标缩短到到原来的
|
“a=1”是“a2=1”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |