题目内容
8.设函数f(x)=|sinx|的图象与直线y=kx(k>0)有且仅有三个公共点,这三个公共点横坐标的最大值为α,则α等于( )| A. | tanα | B. | -cosα | C. | sinα | D. | π |
分析 根据题意,画出图象,然后根据切线斜率的定义以及斜率公式,求得-$\frac{sinα}{α}$=-cosα,由此可得α的值.
解答 解:如图所示: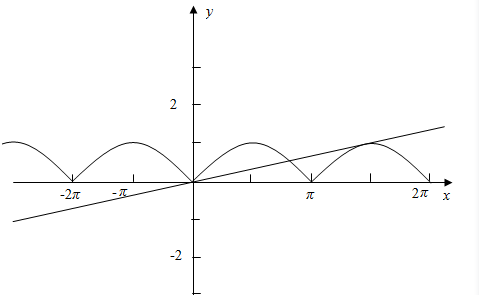
∵函数f(x)=|sinx|的图象与y=kx仅有三个公共点,
这三个公共点横坐标的最
大值为α,
则α∈(π,$\frac{3π}{2}$).
∵直线y=kx与 y=-sinx
相切,
∴k=-$\frac{-sinα}{α}$,同时,
由 y'=-cosx,
∴k=-cosα.
因此,-$\frac{sinα}{α}$=-cosα,
∴α=tanα,
故选:A.
点评 本题重点考查了三角函数图象与性质、三角函数图象变换等知识,属于中档题.解题关键是数形结合思想在解题中的应用,属于中档题.

练习册系列答案
相关题目
20.对于a,b∈R,定义运算“?”:$a?b=\left\{{\begin{array}{l}{{a^2}-ab,a≤b}\\{{b^2}-ab,a>b}\end{array}}\right.$,设f(x)=(2x-1)?(x-1),且关于x的方程f(x)=t(t∈R)恰有三个互不相等的实数根x1,x2,x3,则x1+x2+x3的取值范围是( )
| A. | $(\frac{{5-\sqrt{3}}}{4},1)$ | B. | $(1,\frac{{5+\sqrt{3}}}{4})$ | C. | $(\frac{1}{2},1)$ | D. | (1,2) |