题目内容
3.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左顶点为A(-2,0),过右焦点F且垂直于长轴的弦长为3.(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线y=kx+m(k<0,m>0)与y轴交于点P,与x轴交于点Q,与椭圆C交于M,N两点,若$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{3}{|PQ|}$,求直线y=kx+m过定点,并求出这个定点坐标.
分析 (Ⅰ)由题意a=2,利用过右焦点F且垂直于长轴的弦长为3,求出b,即可求椭圆C的方程;
(Ⅱ)直线y=kx+m(k<0,m>0)与y轴交于点P(0,m),与x轴交于点Q(-$\frac{m}{k}$,0),设M(x1,y1),N(x2,y2),由$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{3}{|PQ|}$,可得$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{3k}{m}$,y=kx+m代入椭圆方程可得(4k2+3)x2+8kmx+4m2-12=0,利用韦达定理,即可得出结论.
解答 解:(Ⅰ)由题意a=2,设过右焦点F且垂直于长轴的弦为MN,
将M(c,yM)代入椭圆方程可得yM=±$\frac{{b}^{2}}{a}$,
∴$\frac{2{b}^{2}}{a}$=3,∴b2=3,
∴椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)证明:直线y=kx+m(k<0,m>0)与y轴交于点P(0,m),
与x轴交于点Q(-$\frac{m}{k}$,0),
设M(x1,y1),N(x2,y2),则
|PM|=$\sqrt{1+{k}^{2}}$x1,|PN|=$\sqrt{1+{k}^{2}}$x2,|PQ|=-$\sqrt{1+{k}^{2}}$•$\frac{m}{k}$,
∵$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{3}{|PQ|}$,∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{3k}{m}$,
∴$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{3k}{m}$,
y=kx+m代入椭圆方程可得(4k2+3)x2+8kmx+4m2-12=0
∴x1+x2=$\frac{-8km}{3+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
∴$\frac{-8km}{4{m}^{2}-12}$=-$\frac{3k}{m}$,
∵m>0,∴m=3,
∴直线y=kx+m恒过定点,且为点(0,3).
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生析解决问题的能力,属于中档题..

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | tanα | B. | -cosα | C. | sinα | D. | π |
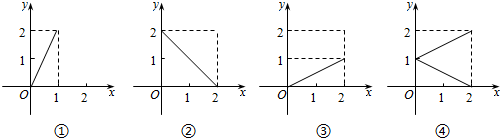
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |